Detta är den fjärde delen i en serie om lösningar på nummerseriegeneratorutmaningen. Stort tack till Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea och Paul White för att du delar med dig av dina idéer och kommentarer.
Jag älskar Paul Whites arbete. Jag blir hela tiden chockad över hans upptäckter och undrar hur fan han kommer på vad han gör. Jag älskar också hans effektiva och vältaliga skrivstil. När jag läser hans artiklar eller inlägg skakar jag ofta på huvudet och säger till min fru Lilach att när jag blir stor vill jag bli precis som Paul.
När jag ursprungligen lade ut utmaningen hoppades jag i hemlighet att Paul skulle lägga upp en lösning. Jag visste att om han gjorde det, skulle det bli en väldigt speciell sådan. Jo, det gjorde han, och det är fascinerande! Den har utmärkt prestanda, och det finns ganska mycket du kan lära dig av den. Den här artikeln är tillägnad Pauls lösning.
Jag ska göra mina tester i tempdb, aktivera I/O och tidsstatistik:
SET NOCOUNT ON; USE tempdb; SET STATISTICS TIME, IO ON;
Begränsningar för tidigare idéer
Att utvärdera tidigare lösningar var en av de viktiga faktorerna för att få bra prestanda möjligheten att använda batchbearbetning. Men har vi utnyttjat det så mycket som möjligt?
Låt oss undersöka planerna för två av de tidigare lösningarna som använde batchbearbetning. I del 1 täckte jag funktionen dbo.GetNumsAlanCharlieItzikBatch, som kombinerade idéer från Alan, Charlie och mig själv.
Här är funktionens definition:
-- Helper dummy table
DROP TABLE IF EXISTS dbo.BatchMe;
GO
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
GO
-- Function definition
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1)
rownum AS rn,
@high + 1 - rownum AS op,
@low - 1 + rownum AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum;
GO Denna lösning definierar en bastabellvärdekonstruktor med 16 rader och en serie kaskadkopplade CTE:er med korskopplingar för att blåsa upp antalet rader till potentiellt 4B. Lösningen använder ROW_NUMBER-funktionen för att skapa bassekvensen av tal i en CTE som kallas Nums, och TOP-filtret för att filtrera önskad nummerseriekardinalitet. För att möjliggöra batchbearbetning använder lösningen en dummy left join med ett falskt villkor mellan Nums CTE och en tabell som heter dbo.BatchMe, som har ett columnstore-index.
Använd följande kod för att testa funktionen med variabeltilldelningstekniken:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
Planutforskarens skildring av den faktiska planen för detta utförande visas i figur 1.
 Figur 1:Plan för dbo.GetNumsAlanCharlieItzikBatch-funktionen
Figur 1:Plan för dbo.GetNumsAlanCharlieItzikBatch-funktionen
När man analyserar batchläge vs radlägesbearbetning är det ganska trevligt att kunna säga bara genom att titta på en plan på hög nivå vilket bearbetningsläge varje operatör använde. Faktum är att Plan Explorer visar en ljusblå batchfigur längst ner till vänster på operatören när dess faktiska körningsläge är Batch. Som du kan se i figur 1 är den enda operatören som använde batch-läge fönsteraggregatoperatorn, som beräknar radnumren. Det finns fortfarande mycket arbete som gjorts av andra operatörer i radläge.
Här är prestationssiffrorna som jag fick i mitt test:
CPU-tid =10032 ms, förfluten tid =10025 ms.logiskt läser 0
För att identifiera vilka operatörer som tog mest tid att köra, använd antingen alternativet Faktisk exekveringsplan i SSMS eller alternativet Hämta faktisk plan i Plan Explorer. Se till att du läser Pauls senaste artikel Understanding Execution Plan Operator Timings. Artikeln beskriver hur man normaliserar de rapporterade operatörskörningstiderna för att få rätt siffror.
I planen i figur 1 spenderas den mesta tiden av de kapslade slingorna längst till vänster och de översta operatörerna, båda körs i radläge. Förutom att radläget är mindre effektivt än batchläget för CPU-intensiva operationer, tänk också på att byte från rad- till batch-läge och tillbaka kräver extra avgifter.
I del 2 täckte jag en annan lösning som använde batchbearbetning, implementerad i funktionen dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2. Denna lösning kombinerade idéer från John Number2, Dave Mason, Joe Obbish, Alan, Charlie och mig själv. Huvudskillnaden mellan den tidigare lösningen och den här är att som basenhet använder den förra en virtuell tabellvärdekonstruktor och den senare använder en faktisk tabell med ett kolumnlagerindex, vilket ger dig batchbearbetning "gratis." Här är koden som skapar tabellen och fyller den med en INSERT-sats med 102 400 rader för att få den att komprimeras:
DROP TABLE IF EXISTS dbo.NullBits102400;
GO
CREATE TABLE dbo.NullBits102400
(
b BIT NULL,
INDEX cc_NullBits102400 CLUSTERED COLUMNSTORE
WITH (DATA_COMPRESSION = COLUMNSTORE_ARCHIVE)
);
GO
WITH
L0 AS (SELECT CAST(NULL AS BIT) AS b
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1),(1)) AS D(b)),
L1 AS (SELECT A.b FROM L0 AS A CROSS JOIN L0 AS B),
nulls(b) AS (SELECT A.b FROM L1 AS A CROSS JOIN L1 AS B CROSS JOIN L1 AS C)
INSERT INTO dbo.NullBits102400 WITH (TABLOCK) (b)
SELECT TOP(102400) b FROM nulls;
GO Här är funktionens definition:
CREATE OR ALTER FUNCTION dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2
(@low AS BIGINT = 1, @high AS BIGINT) RETURNS TABLE
AS
RETURN
WITH
Nums AS (SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM dbo.NullBits102400 AS A
CROSS JOIN dbo.NullBits102400 AS B)
SELECT TOP(@high - @low + 1)
rownum AS rn,
@high + 1 - rownum AS op,
@low - 1 + rownum AS n
FROM Nums
ORDER BY rownum;
GO En enda korskoppling mellan två instanser av basbordet är tillräckligt för att producera långt över den önskade potentialen för 4B-rader. Återigen här använder lösningen ROW_NUMBER-funktionen för att producera bassekvensen av tal och TOP-filtret för att begränsa önskad nummerseriekardinalitet.
Här är koden för att testa funktionen med variabeltilldelningstekniken:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);
Planen för detta utförande visas i figur 2.
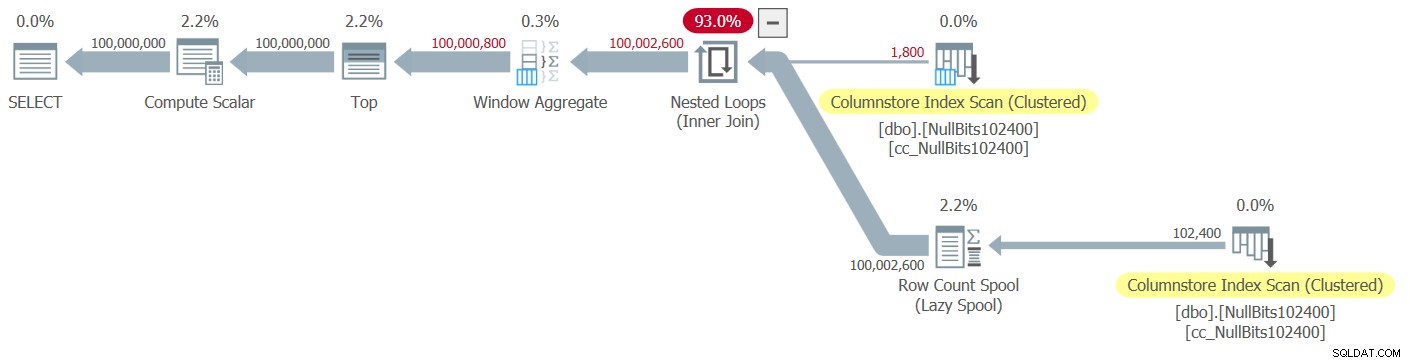 Figur 2:Plan för dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2-funktionen
Figur 2:Plan för dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2-funktionen
Observera att endast två operatörer i den här planen använder batch-läge – den översta skanningen av tabellens klustrade kolumnlagerindex, som används som den yttre inmatningen av Nested Loops-kopplingen, och Window Aggregate-operatorn, som används för att beräkna basradnumren .
Jag fick följande prestationssiffror för mitt test:
CPU-tid =9812 ms, förfluten tid =9813 ms.Tabell 'NullBits102400'. Skanningsantal 2, logiskt läser 0, fysiskt läser 0, sidserver läser 0, read-ahead läser 0, sidserver läser framåt läser 0, lob logiskt läser 8, lob fysisk läser 0, lob sidserver läser 0, lob läs- ahead läser 0, lob page server read-ahead läser 0.
Tabell 'NullBits102400'. Segment visar 2, segment hoppade över 0.
Återigen, den mesta tiden för att genomföra denna plan spenderas av de kapslade loopar och toppoperatörer längst till vänster, som körs i radläge.
Pauls lösning
Innan jag presenterar Pauls lösning ska jag börja med min teori angående tankeprocessen han gick igenom. Detta är faktiskt en bra inlärningsövning, och jag föreslår att du går igenom den innan du tittar på lösningen. Paul insåg de försvagande effekterna av en plan som blandar både batch- och radlägen, och ställde en utmaning för sig själv att komma på en lösning som får en hel-batch-mode-plan. Om den lyckas är potentialen för att en sådan lösning ska fungera bra ganska hög. Det är verkligen spännande att se om ett sådant mål ens kan uppnås med tanke på att det fortfarande finns många operatörer som ännu inte stöder batchläge och många faktorer som hämmar batchbearbetning. Till exempel, i skrivande stund är den enda join-algoritmen som stöder batch-bearbetning hash join-algoritmen. En korskoppling optimeras med hjälp av algoritmen för kapslade loopar. Dessutom är Top-operatören för närvarande implementerad endast i radläge. Dessa två element är viktiga grundläggande element som används i planerna för många av de lösningar som jag hittills täckt, inklusive de två ovan.
Om du antar att du gav utmaningen att skapa en lösning med en plan för all-batch-läge ett anständigt försök, låt oss gå vidare till den andra övningen. Jag kommer först att presentera Pauls lösning som han gav den, med hans inline-kommentarer. Jag kommer också att köra det för att jämföra dess prestanda med de andra lösningarna. Jag lärde mig mycket genom att dekonstruera och rekonstruera hans lösning, ett steg i taget, för att se till att jag noggrant förstod varför han använde var och en av de tekniker han gjorde. Jag föreslår att du gör detsamma innan du går vidare och läser mina förklaringar.
Här är Pauls lösning, som involverar en hjälpkolumnlagertabell som heter dbo.CS och en funktion som heter dbo.GetNums_SQLkiwi:
-- Helper columnstore table
DROP TABLE IF EXISTS dbo.CS;
-- 64K rows (enough for 4B rows when cross joined)
-- column 1 is always zero
-- column 2 is (1...65536)
SELECT
-- type as integer NOT NULL
-- (everything is normalized to 64 bits in columnstore/batch mode anyway)
n1 = ISNULL(CONVERT(integer, 0), 0),
n2 = ISNULL(CONVERT(integer, N.rn), 0)
INTO dbo.CS
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@SPID)
FROM master.dbo.spt_values AS SV1
CROSS JOIN master.dbo.spt_values AS SV2
ORDER BY
rn ASC
OFFSET 0 ROWS
FETCH NEXT 65536 ROWS ONLY
) AS N;
-- Single compressed rowgroup of 65,536 rows
CREATE CLUSTERED COLUMNSTORE INDEX CCI
ON dbo.CS
WITH (MAXDOP = 1);
GO
-- The function
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
@low bigint = 1,
@high bigint
)
RETURNS table
AS
RETURN
SELECT
N.rn,
n = @low - 1 + N.rn,
op = @high + 1 - N.rn
FROM
(
SELECT
-- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
-- Batch mode hash cross join
-- Integer not null data type avoid hash probe residual
-- This is always 0 = 0
ON N2.n1 = N1.n1
WHERE
-- Try to avoid SQRT on negative numbers and enable simplification
-- to single constant scan if @low > @high (with literals)
-- No start-up filters in batch mode
@high >= @low
-- Coarse filter:
-- Limit each side of the cross join to SQRT(target number of rows)
-- IIF avoids SQRT on negative numbers with parameters
AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
) AS N
WHERE
-- Precise filter:
-- Batch mode filter the limited cross join to the exact number of rows needed
-- Avoids the optimizer introducing a row-mode Top with following row mode compute scala
@low - 2 + N.rn < @high;
GO Här är koden jag använde för att testa funktionen med variabeltilldelningstekniken:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000);
Jag fick planen som visas i figur 3 för mitt test.
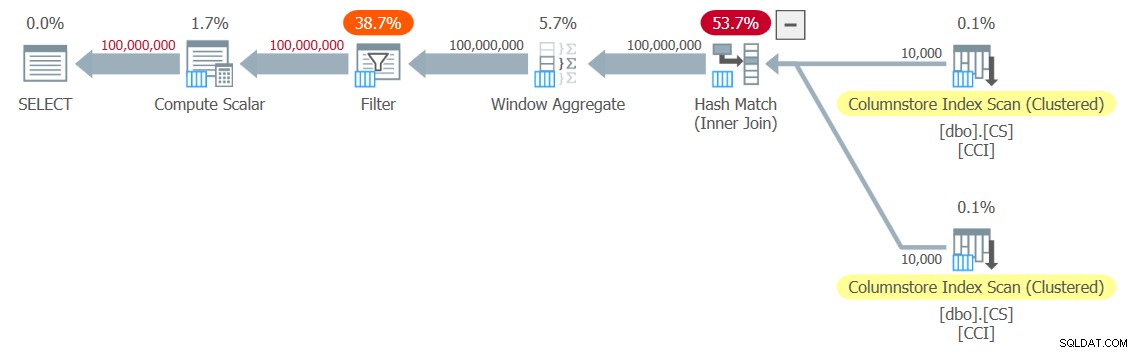 Figur 3:Plan för dbo.GetNums_SQLkiwi-funktionen
Figur 3:Plan för dbo.GetNums_SQLkiwi-funktionen
Det är en hel-batch-mode-plan! Det är ganska imponerande.
Här är prestandasiffrorna som jag fick för det här testet på min maskin:
CPU-tid =7812 ms, förfluten tid =7876 ms.Tabell 'CS'. Scan count 2, logiskt läser 0, fysiskt läser 0, sidserver läser 0, läs framåt läser 0, sidserver läser framåt läser 0, lob logiskt läser 44, lob fysisk läser 0, lob sidserver läser 0, lob läs- ahead läser 0, lob page server read-ahead läser 0.
Tabell 'CS'. Segment visar 2, segment hoppade över 0.
Låt oss också verifiera att om du behöver returnera siffrorna ordnade efter n, är lösningen ordningsbevarande med avseende på rn - åtminstone när du använder konstanter som indata - och därmed undvika explicit sortering i planen. Här är koden för att testa den med beställning:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000) ORDER BY n;
Du får samma plan som i figur 3, och därför liknande prestandasiffror:
CPU-tid =7765 ms, förfluten tid =7822 ms.Tabell 'CS'. Scan count 2, logiskt läser 0, fysiskt läser 0, sidserver läser 0, läs framåt läser 0, sidserver läser framåt läser 0, lob logiskt läser 44, lob fysisk läser 0, lob sidserver läser 0, lob läs- ahead läser 0, lob page server read-ahead läser 0.
Tabell 'CS'. Segment visar 2, segment hoppade över 0.
Det är en viktig sida av lösningen.
Ändra vår testmetod
Pauls lösnings prestanda är en anständig förbättring i både förfluten tid och CPU-tid jämfört med de två tidigare lösningarna, men det verkar inte som den mer dramatiska förbättringen man kan förvänta sig av en plan för batchläge. Vi kanske saknar något?
Låt oss försöka analysera operatörens utförandetider genom att titta på den faktiska exekveringsplanen i SSMS som visas i figur 4.
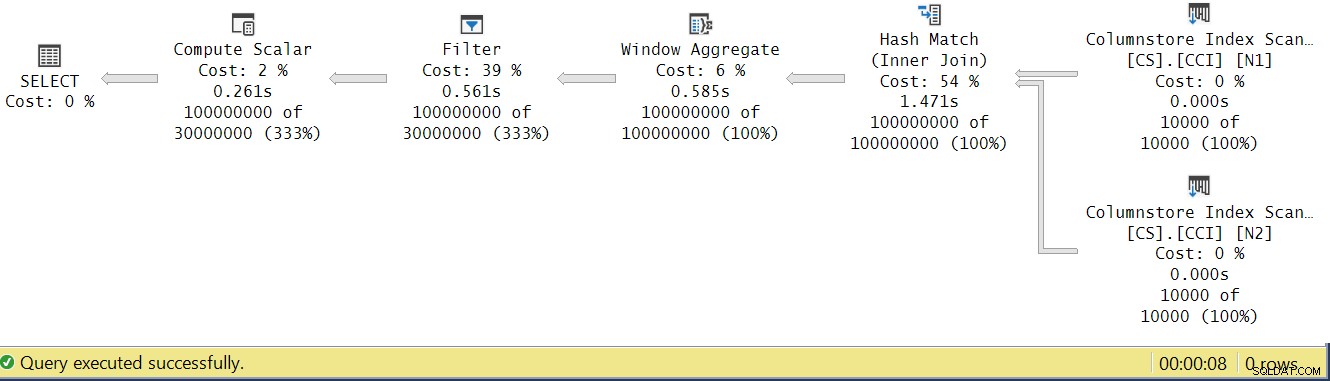 Figur 4:Operatörs körtider för dbo.GetNums_SQLkiwi-funktionen
Figur 4:Operatörs körtider för dbo.GetNums_SQLkiwi-funktionen
I Pauls artikel om att analysera operatörskörningstider förklarar han att med batchlägesoperatörer rapporterar var och en sin egen körningstid. Om du summerar exekveringstiderna för alla operatörer i denna faktiska plan får du 2,878 sekunder, men planen tog 7,876 att genomföra. 5 sekunder av exekveringstiden verkar saknas. Svaret på detta ligger i testtekniken som vi använder, med variabeltilldelningen. Kom ihåg att vi bestämde oss för att använda den här tekniken för att eliminera behovet av att skicka alla rader från servern till den som ringer och för att undvika de I/O som skulle vara involverade i att skriva resultatet till en tabell. Det verkade vara det perfekta alternativet. Den verkliga kostnaden för variabeltilldelningen är dock gömd i den här planen, och den körs naturligtvis i radläge. Mysteriet löst.
Uppenbarligen i slutet av dagen är ett bra test ett test som adekvat återspeglar din produktionsanvändning av lösningen. Om du vanligtvis skriver data till en tabell behöver du ditt test för att återspegla det. Om du skickar resultatet till den som ringer behöver du ditt test för att återspegla det. Variabeltilldelningen tycks i alla fall representera en stor del av exekveringstiden i vårt test, och det är helt klart osannolikt att representera typisk produktionsanvändning av funktionen. Paul föreslog att istället för variabeltilldelning kunde testet tillämpa ett enkelt aggregat som MAX på den returnerade nummerkolumnen (n/rn/op). En aggregatoperatör kan använda batchbearbetning, så planen skulle inte involvera konvertering från batch- till radläge som ett resultat av dess användning, och dess bidrag till den totala körtiden bör vara ganska litet och känt.
Så låt oss testa om alla tre lösningar som behandlas i den här artikeln. Här är koden för att testa funktionen dbo.GetNumsAlanCharlieItzikBatch:
SELECT MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);
Jag fick planen som visas i figur 5 för detta test.
 Figur 5:Plan för dbo.GetNumsAlanCharlieItzikBatch-funktion med aggregerad
Figur 5:Plan för dbo.GetNumsAlanCharlieItzikBatch-funktion med aggregerad
Här är prestationssiffrorna som jag fick för det här testet:
CPU-tid =8469 ms, förfluten tid =8733 ms.logiskt läser 0
Observera att körtiden sjönk från 10,025 sekunder med variabeltilldelningstekniken till 8,733 med den aggregerade tekniken. Det är en bit över en sekund av exekveringstid som vi kan tillskriva variabeltilldelningen här.
Här är koden för att testa funktionen dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2:
SELECT MAX(n) AS mx FROM dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2(1, 100000000) OPTION(MAXDOP 1);
Jag fick planen som visas i figur 6 för detta test.
 Figur 6:Plan för dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2-funktionen med aggregate
Figur 6:Plan för dbo.GetNumsJohn2DaveObbishAlanCharlieItzik2-funktionen med aggregate
Här är prestationssiffrorna som jag fick för det här testet:
CPU-tid =7031 ms, förfluten tid =7053 ms.Tabell 'NullBits102400'. Skanningsantal 2, logiskt läser 0, fysiskt läser 0, sidserver läser 0, read-ahead läser 0, sidserver läser framåt läser 0, lob logiskt läser 8, lob fysisk läser 0, lob sidserver läser 0, lob läs- ahead läser 0, lob page server read-ahead läser 0.
Tabell 'NullBits102400'. Segment visar 2, segment hoppade över 0.
Observera att körtiden sjönk från 9,813 sekunder med variabeltilldelningstekniken till 7,053 med den aggregerade tekniken. Det är lite över två sekunders exekveringstid som vi kan tillskriva variabeltilldelningen här.
Och här är koden för att testa Pauls lösning:
SELECT MAX(n) AS mx FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);
Jag får planen som visas i figur 7 för detta test.
 Figur 7:Plan för dbo.GetNums_SQLkiwi-funktion med aggregat
Figur 7:Plan för dbo.GetNums_SQLkiwi-funktion med aggregat
Och nu till det stora ögonblicket. Jag fick följande prestationssiffror för det här testet:
CPU-tid =3125 ms, förfluten tid =3149 ms.Tabell 'CS'. Scan count 2, logiskt läser 0, fysiskt läser 0, sidserver läser 0, läs framåt läser 0, sidserver läser framåt läser 0, lob logiskt läser 44, lob fysisk läser 0, lob sidserver läser 0, lob läs- ahead läser 0, lob page server read-ahead läser 0.
Tabell 'CS'. Segment visar 2, segment hoppade över 0.
Körtiden sjönk från 7,822 sekunder till 3,149 sekunder! Låt oss undersöka operatörens utförandetider i den faktiska planen i SSMS, som visas i figur 8.
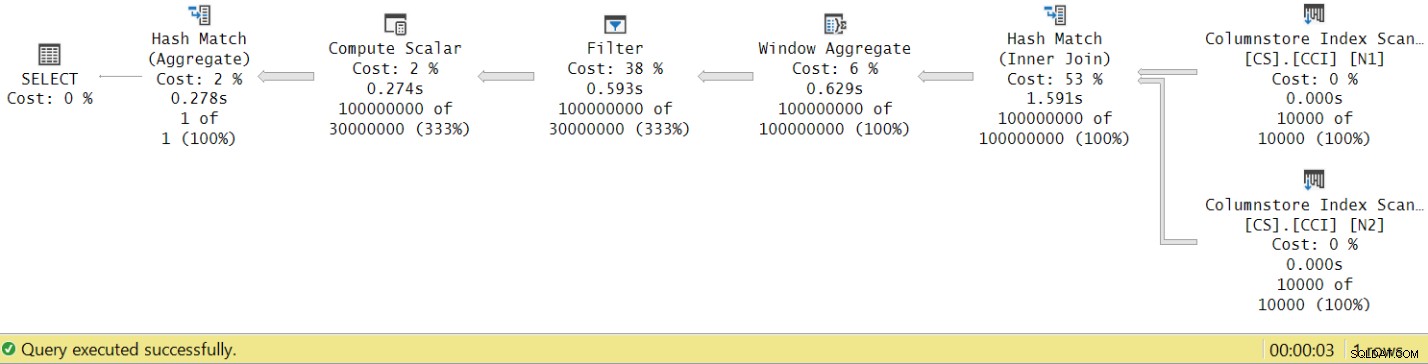 Figur 8:Operatörskörningstider för dbo.GetNums-funktionen med aggregat
Figur 8:Operatörskörningstider för dbo.GetNums-funktionen med aggregat
Om du nu ackumulerar genomförandetiderna för de enskilda operatörerna kommer du att få ett liknande antal som den totala planens genomförandetid.
Figur 9 har en prestandajämförelse i termer av förfluten tid mellan de tre lösningarna med användning av både variabel tilldelning och aggregerad testteknik.
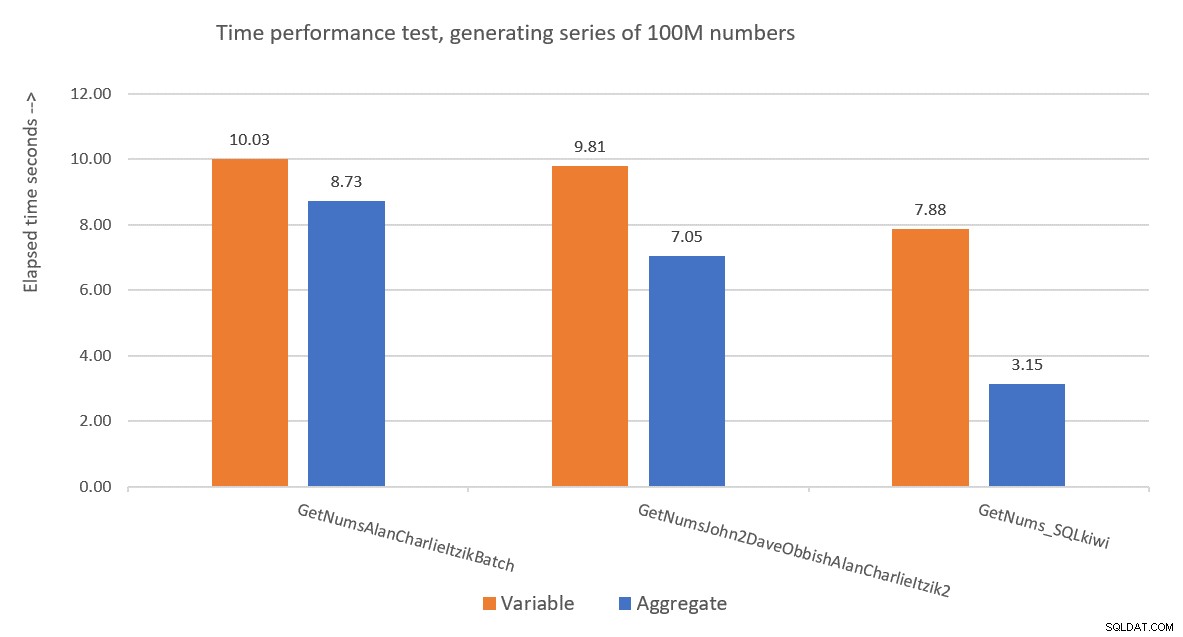 Figur 9:Prestandajämförelse
Figur 9:Prestandajämförelse
Pauls lösning är en klar vinnare, och detta är särskilt uppenbart när man använder aggregattestningstekniken. Vilken imponerande bedrift!
Dekonstruerar och rekonstruerar Pauls lösning
Att dekonstruera och sedan rekonstruera Pauls lösning är en fantastisk övning, och du får lära dig mycket medan du gör det. Som föreslagits tidigare rekommenderar jag att du går igenom processen själv innan du fortsätter läsa.
Det första valet du behöver göra är den teknik som du skulle använda för att generera det önskade potentiella antalet rader av 4B. Paul valde att använda en kolumnlagertabell och fylla den med så många rader som kvadratroten av det erforderliga numret, vilket betyder 65 536 rader, så att du med en enda korskoppling skulle få det antal som krävs. Du kanske tänker att med färre än 102 400 rader skulle du inte få en komprimerad radgrupp, men detta gäller när du fyller i tabellen med en INSERT-sats som vi gjorde med tabellen dbo.NullBits102400. Det gäller inte när du skapar ett kolumnlagerindex på en förifylld tabell. Så Paul använde en SELECT INTO-sats för att skapa och fylla i tabellen som en radlagringsbaserad hög med 65 536 rader och skapade sedan ett klustrat kolumnlagerindex, vilket resulterade i en komprimerad radgrupp.
Nästa utmaning är att ta reda på hur man får en korskoppling att bearbetas med en batchlägesoperatör. För detta behöver du att join-algoritmen är hash. Kom ihåg att en korskoppling är optimerad med algoritmen för kapslade loopar. Du måste på något sätt lura optimeraren att tro att du använder en inre equijoin (hash kräver minst ett likhetsbaserat predikat), men få en cross join i praktiken.
Ett uppenbart första försök är att använda en inre sammanfogning med ett artificiellt sammanfogningspredikat som alltid är sant, som så:
SELECT *
FROM dbo.CS AS N1
INNER HASH JOIN dbo.CS AS N2
ON 0 = 0; Men den här koden misslyckas med följande fel:
Msg 8622, Level 16, State 1, Line 246Frågeprocessor kunde inte skapa en frågeplan på grund av tipsen som definieras i denna fråga. Skicka frågan igen utan att ange några tips och utan att använda SET FORCEPLAN.
SQL Servers optimerare känner igen att detta är ett artificiellt inre kopplingspredikat, förenklar den inre kopplingen till en korskoppling och ger ett felmeddelande som säger att den inte kan hantera tipset att tvinga fram en hashkopplingsalgoritm.
För att lösa detta skapade Paul en INT NOT NULL-kolumn (mer om varför denna specifikation inom kort) kallad n1 i sin dbo.CS-tabell och fyllde den med 0 i alla rader. Han använde sedan join-predikatet N2.n1 =N1.n1, och fick i praktiken propositionen 0 =0 i alla matchningsutvärderingar, samtidigt som han uppfyllde minimikraven för en hash join-algoritm.
Detta fungerar och producerar en plan för all-batch-läge:
SELECT *
FROM dbo.CS AS N1
INNER HASH JOIN dbo.CS AS N2
ON N2.n1 = N1.n1; Angående anledningen till att n1 definieras som INT NOT NULL; varför förbjuda NULLs och varför inte använda BIGINT? Anledningen till dessa val är att undvika en rest av hash-sond (ett extra filter som appliceras av hash-join-operatören utöver det ursprungliga join-predikatet), vilket kan resultera i extra onödiga kostnader. Se Pauls artikel Gå med i prestanda, implicita omvandlingar och rester för detaljer. Här är den del av artikeln som är relevant för oss:
"Om kopplingen är på en enskild kolumn skrivs som tinyint, smallint eller heltal och om båda kolumnerna är begränsade till att vara INTE NULL, är hashfunktionen "perfekt" - vilket betyder att det inte finns någon chans för en hashkollision, och frågeprocessorn behöver inte kontrollera värdena igen för att säkerställa att de verkligen matchar.Observera att denna optimering inte gäller för stora kolumner."
För att kontrollera denna aspekt, låt oss skapa en annan tabell som heter dbo.CS2 med en nollbar n1-kolumn:
DROP TABLE IF EXISTS dbo.CS2; SELECT * INTO dbo.CS2 FROM dbo.CS; ALTER TABLE dbo.CS2 ALTER COLUMN n1 INT NULL; CREATE CLUSTERED COLUMNSTORE INDEX CCI ON dbo.CS2 WITH (MAXDOP = 1);
Låt oss först testa en fråga mot dbo.CS (där n1 definieras som INT NOT NULL), generera 4B basradnummer i en kolumn som kallas rn och tillämpa MAX-aggregatet på kolumnen:
SELECT
mx = MAX(N.rn)
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
ON N2.n1 = N1.n1
) AS N; Vi kommer att jämföra planen för den här frågan med planen för en liknande fråga mot dbo.CS2 (där n1 är definierad som INT NULL):
SELECT
mx = MAX(N.rn)
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
FROM dbo.CS2 AS N1
JOIN dbo.CS2 AS N2
ON N2.n1 = N1.n1
) AS N; Planerna för båda frågorna visas i figur 10.
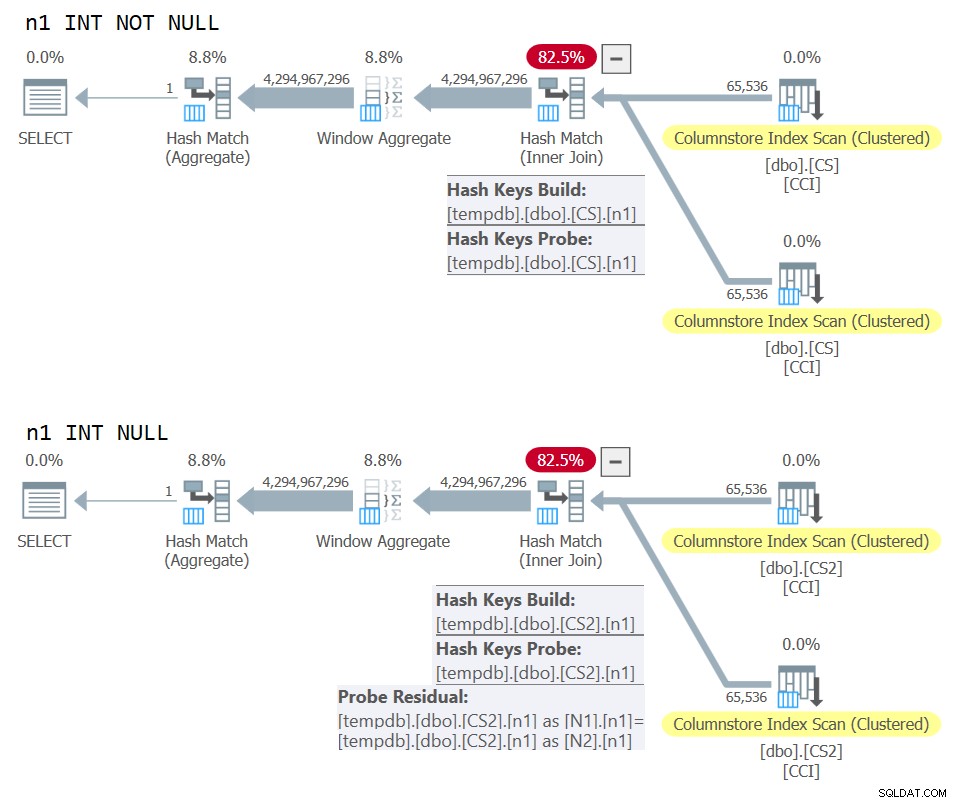 Figur 10:Planjämförelse för NOT NULL vs NULL join-nyckel
Figur 10:Planjämförelse för NOT NULL vs NULL join-nyckel
Du kan tydligt se den extra sondresten som appliceras i den andra planen men inte den första.
På min maskin slutfördes frågan mot dbo.CS på 91 sekunder, och frågan mot dbo.CS2 klar på 92 sekunder. I Pauls artikel rapporterar han en skillnad på 11 % till förmån för NOT NULL-fallet för exemplet han använde.
BTW, de av er med ett skarpt öga kommer att ha lagt märke till användningen av ORDER BY @@TRANCOUNT som ROW_NUMBER-funktionens beställningsspecifikation. Om du noggrant läser Pauls inline-kommentarer i hans lösning, nämner han att användningen av funktionen @@TRANCOUNT är en parallellismhämmare, medan användningen av @@SPID inte är det. Så du kan använda @@TRANCOUNT som körtidskonstant i beställningsspecifikationen när du vill tvinga fram en serieplan och @@SPID när du inte gör det.
Som nämnt tog det frågan mot dbo.CS 91 sekunder att köra på min maskin. Vid det här laget kan det vara intressant att testa samma kod med en äkta korskoppling, så att optimeraren kan använda en algoritm för kapslade loopar i radläge:
SELECT
mx = MAX(N.rn)
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
FROM dbo.CS AS N1
CROSS JOIN dbo.CS AS N2
) AS N; Det tog den här koden 104 sekunder att slutföra på min maskin. Så vi får en avsevärd prestandaförbättring med batch-mode hash join.
Vårt nästa problem är det faktum att när du använder TOP för att filtrera önskat antal rader, får du en plan med en row-mode Top-operatör. Här är ett försök att implementera funktionen dbo.GetNums_SQLkiwi med ett TOP-filter:
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
@low bigint = 1,
@high bigint
)
RETURNS table
AS
RETURN
SELECT
N.rn,
n = @low - 1 + N.rn,
op = @high + 1 - N.rn
FROM
(
SELECT TOP (100000000 - 1 + 1)
rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
ON N2.n1 = N1.n1
ORDER BY rn
) AS N;
GO Låt oss testa funktionen:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);
Jag fick planen som visas i figur 11 för detta test.
 Figur 11:Planera med TOP-filter
Figur 11:Planera med TOP-filter
Observera att Top-operatören är den enda i planen som använder radlägesbearbetning.
Jag fick följande tidsstatistik för denna körning:
CPU-tid =6078 ms, förfluten tid =6071 ms.Den största delen av körtiden i denna plan spenderas av row-mode Top-operatören och det faktum att planen måste gå igenom batch-to-row-mode-konvertering och tillbaka.
Vår utmaning är att hitta ett batch-mode-filtreringsalternativ till rad-mode TOP. Predikatbaserade filter som de som tillämpas med WHERE-satsen kan potentiellt hanteras med batchbearbetning.
Pauls tillvägagångssätt var att introducera en andra INT-typad kolumn (se inline-kommentaren "allt är ändå normaliserat till 64-bitar i kolumnlagrings-/batchläge" ) anropade n2 till tabellen dbo.CS och fyll i den med heltalssekvensen 1 till 65 536. I lösningens kod använde han två predikatbaserade filter. Det ena är ett grovt filter i den inre frågan med predikat som involverar kolumnen n2 från båda sidor av kopplingen. Detta grovfilter kan resultera i vissa falska positiva resultat. Här är det första förenklade försöket med ett sådant filter:
WHERE
-- Coarse filter:
N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1)))) Med ingångarna 1 och 100 000 000 som @låg och @hög får du inga falska positiva resultat. Men försök med 1 och 100 000 001, så får du några. Du får en sekvens med 100 020 001 nummer istället för 100 000 001.
För att eliminera de falska positiva, lade Paul till ett andra, exakt, filter som involverade kolumnen rn i den yttre frågan. Här är det första förenklade försöket med ett så exakt filter:
WHERE
-- Precise filter:
N.rn < @high - @low + 2 Låt oss revidera definitionen av funktionen för att använda ovanstående predikatbaserade filter istället för TOP, ta 1:
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
@low bigint = 1,
@high bigint
)
RETURNS table
AS
RETURN
SELECT
N.rn,
n = @low - 1 + N.rn,
op = @high + 1 - N.rn
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
ON N2.n1 = N1.n1
WHERE
-- Coarse filter:
N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
) AS N
WHERE
-- Precise filter:
N.rn < @high - @low + 2;
GO Låt oss testa funktionen:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);
Jag fick planen som visas i figur 12 för detta test.
 Figur 12:Planera med WHERE-filter, ta 1
Figur 12:Planera med WHERE-filter, ta 1
Tyvärr gick något helt klart fel. SQL Server konverterade vårt predikatbaserade filter som involverade kolumnen rn till ett TOP-baserat filter och optimerade det med en Top-operator – vilket är precis vad vi försökte undvika. För att lägga förolämpning till skada bestämde optimeraren också att använda algoritmen för kapslade loopar för sammanfogningen.
Det tog den här koden 18,8 sekunder att slutföra på min maskin. Ser inte bra ut.
Angående de kapslade loops join, detta är något som vi enkelt skulle kunna ta hand om med hjälp av en join-tips i den inre frågan. Bara för att se prestandapåverkan, här är ett test med en påtvingad hash-anslutningsfrågetips som används i själva testfrågan:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(HASH JOIN);
Körtiden minskar till 13,2 sekunder.
Vi har fortfarande problemet med konverteringen av WHERE-filtret mot rn till ett TOP-filter. Låt oss försöka förstå hur detta hände. Vi använde följande filter i den yttre frågan:
WHERE N.rn < @high - @low + 2
Kom ihåg att rn representerar ett omanipulerat ROW_NUMBER-baserat uttryck. Ett filter baserat på att ett sådant omanipulerat uttryck ligger i ett givet intervall optimeras ofta med en Top-operator, vilket för oss är dåliga nyheter på grund av användningen av radlägesbehandling.
Pauls lösning var att använda ett likvärdigt predikat, men ett som tillämpar manipulation på rn, som så:
WHERE @low - 2 + N.rn < @high
Filtrering av ett uttryck som lägger till manipulation till ett ROW_NUMBER-baserat uttryck hämmar konverteringen av det predikatbaserade filtret till ett TOP-baserat. Det är lysande!
Låt oss revidera funktionens definition för att använda ovanstående WHERE-predikat, ta 2:
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
@low bigint = 1,
@high bigint
)
RETURNS table
AS
RETURN
SELECT
N.rn,
n = @low - 1 + N.rn,
op = @high + 1 - N.rn
FROM
(
SELECT
rn = ROW_NUMBER() OVER (ORDER BY @@TRANCOUNT ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
ON N2.n1 = N1.n1
WHERE
-- Coarse filter:
N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
) AS N
WHERE
-- Precise filter:
@low - 2 + N.rn < @high;
GO Testa funktionen igen, utan några speciella tips eller något:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);
Den får naturligtvis en hel-batch-mode-plan med en hash join-algoritm och ingen toppoperatör, vilket resulterar i en exekveringstid på 3,177 sekunder. Ser bra ut.
Nästa steg är att kontrollera om lösningen hanterar dåliga ingångar bra. Låt oss prova det med ett negativt delta:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);
Denna exekvering misslyckas med följande fel.
Msg 3623, Level 16, State 1, Line 436En ogiltig flyttalsoperation inträffade.
Felet beror på försöket att tillämpa en kvadratrot ur ett negativt tal.
Pauls lösning innebar två tillägg. En är att lägga till följande predikat till den inre frågans WHERE-sats:
@high >= @low
Detta filter gör mer än vad det verkar från början. Om du har läst Pauls inline-kommentarer noggrant kan du hitta den här delen:
"Försök att undvika SQRT på negativa siffror och möjliggör förenkling av enkel konstant skanning om @låg> @hög (med bokstaver). Inga startfilter i batchläge."Den spännande delen här är möjligheten att använda en konstant skanning med konstanter som indata. Jag kommer till det här snart.
Det andra tillägget är att tillämpa IIF-funktionen på inmatningsuttrycket på SQRT-funktionen. Detta görs för att undvika negativ inmatning när man använder icke-konstanter som indata till vår sifferfunktion, och om optimeraren bestämmer sig för att hantera predikatet som involverar SQRT före predikatet @high>=@low.
Innan IIF-tillägget, till exempel, såg predikatet som involverade N1.n2 ut så här:
N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, @high - @low + 1))))
After adding IIF, it looks like this:
N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
With these two additions, we’re now basically ready for the final definition of the dbo.GetNums_SQLkiwi function:
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
@low bigint = 1,
@high bigint
)
RETURNS table
AS
RETURN
SELECT
N.rn,
n = @low - 1 + N.rn,
op = @high + 1 - N.rn
FROM
(
SELECT
-- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
FROM dbo.CS AS N1
JOIN dbo.CS AS N2
-- Batch mode hash cross join
-- Integer not null data type avoid hash probe residual
-- This is always 0 = 0
ON N2.n1 = N1.n1
WHERE
-- Try to avoid SQRT on negative numbers and enable simplification
-- to single constant scan if @low > @high (with literals)
-- No start-up filters in batch mode
@high >= @low
-- Coarse filter:
-- Limit each side of the cross join to SQRT(target number of rows)
-- IIF avoids SQRT on negative numbers with parameters
AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
) AS N
WHERE
-- Precise filter:
-- Batch mode filter the limited cross join to the exact number of rows needed
-- Avoids the optimizer introducing a row-mode Top with following row mode compute scalar
@low - 2 + N.rn < @high;
GO Now back to the comment about the constant scan. When using constants that result in a negative range as inputs to the function, e.g., 100,000,000 and 1 as @low and @high, after parameter embedding the WHERE filter of the inner query looks like this:
WHERE
1 >= 100000000
AND ... The whole plan can then be simplified to a single Constant Scan operator. Prova det:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(100000000, 1);
The plan for this execution is shown in Figure 13.
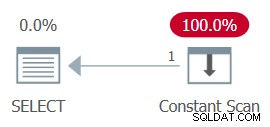 Figure 13:Plan with constant scan
Figure 13:Plan with constant scan
Unsurprisingly, I got the following performance numbers for this execution:
CPU time =0 ms, elapsed time =0 ms.logical reads 0
When passing a negative range with nonconstants as inputs, the use of the IIF function will prevent any attempt to compute a square root of a negative input.
Now let’s test the function with a valid input range:
SELECT MAX(n) FROM dbo.GetNums_SQLkiwi(1, 100000000);
You get the all-batch-mode plan shown in Figure 14.
 Figure 14:Plan for dbo.GetNums_SQLkiwi function
Figure 14:Plan for dbo.GetNums_SQLkiwi function
This is the same plan you saw earlier in Figure 7.
I got the following time statistics for this execution:
CPU time =3000 ms, elapsed time =3111 ms.Ladies and gentlemen, I think we have a winner! :)
Slutsats
I’ll have what Paul’s having.
Are we done yet, or is this series going to last forever?
No and no.
