Utmaningslösningar för nummerseriegenerator – del 5

Detta är den femte och sista delen i serien som täcker lösningar på nummerseriegeneratorutmaningen. I del 1, del 2, del 3 och del 4 behandlade jag rena T-SQL-lösningar. Tidigt när jag lade upp pusslet kommenterade flera personer att den bästa lösningen troligen skulle vara en CLR-baserad. I den här artikeln kommer vi att testa detta intuitiva antagande. Specifikt kommer jag att täcka CLR-baserade lösningar publicerade av Kamil Kosno och Adam Machanic.

Stort tack till Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea och Paul White för att du delar med dig av dina idéer och kommentarer.

Jag ska göra mina tester i en databas som heter testdb. Använd följande kod för att skapa databasen om den inte finns, och för att aktivera I/O- och tidsstatistik:

-- DB and statsSET NOCOUNT ON;SET STATISTICS IO, TIME ON;GO IF DB_ID('testdb') IS NULL SKAPA DATABAS testdb;GO ANVÄND testdb;GO

För enkelhetens skull inaktiverar jag CLR strikt säkerhet och gör databasen pålitlig med hjälp av följande kod:

-- Aktivera CLR, inaktivera CLR strikt säkerhet och gör db trustworthyEXEC sys.sp_configure 'visa avancerade inställningar', 1;RECONFIGURE; EXEC sys.sp_configure 'clr aktiverad', 1;EXEC sys.sp_configure 'clr strikt säkerhet', 0;RECONFIGURE; EXEC sys.sp_configure 'visa avancerade inställningar', 0;RECONFIGURE; ALTER DATABASE testdb STÄLL PÅ TROLIGT; GÅ

Tidigare lösningar

Innan jag tar upp de CLR-baserade lösningarna, låt oss snabbt granska prestandan för två av de bäst presterande T-SQL-lösningarna.

Den bäst presterande T-SQL-lösningen som inte använde några beständiga bastabeller (förutom den tomma kolumnlagertabellen för att få batchbearbetning), och därför inte involverade några I/O-operationer, var den som implementerades i funktionen dbo.GetNumsAlanCharlieItzikBatch. Jag täckte denna lösning i del 1.

Här är koden för att skapa den tomma kolumnlagertabellen som funktionens fråga använder:

SLAPP TABELL OM FINNS dbo.BatchMe;GO SKAPA TABELL dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);GO

Och här är koden med funktionens definition:

SKAPA ELLER ÄNDRA FUNKTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT =1, @high AS BIGINT) RETURER TABLEASRETURN MED L0 AS (VÄLJ 1 AS c FROM (VÄRDEN(1),(1),(1),(1) ),(1),(1),(1),(1), (1),(1),(1),(1),(1),(1),(1),(1)) SOM D(c) ), L1 AS ( VÄLJ 1 AS c FRÅN L0 SOM EN KORSKOPPLING L0 AS B ), L2 AS ( VÄLJ 1 AS c FRÅN L1 SOM EN KORSKOPPLING L1 AS B ), L3 AS ( VÄLJ 1 AS c FRÅN L2 SOM KORSA JOIN L2 AS B ), Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum FROM L3 ) SELECT TOP(@high - @low + 1) rownum AS rn, @high + 1 - rownum AS op, @low - 1 + rownum AS n FROM Nums VÄNSTER YTTRE JOIN dbo.BatchMe ON 1 =0 BESTÄLL EFTER rownum;GO

Låt oss först testa funktionen som begär en serie med 100 miljoner nummer, med MAX-aggregatet tillämpat på kolumn n:

VÄLJ MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

Kom ihåg att den här testtekniken undviker att sända 100 miljoner rader till den som ringer och undviker också den radmode som är involverad i variabeltilldelning när man använder tekniken för variabeltilldelning.

Här är tidsstatistiken som jag fick för det här testet på min maskin:

Utförandet av denna funktion ger inga logiska läsningar, naturligtvis.

Låt oss sedan testa det i ordning med hjälp av variabeltilldelningstekniken:

DEKLARE @n SOM STOR; VÄLJ @n =n FRÅN dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) BESTÄLL EFTER n OPTION(MAXDOP 1);

Jag fick följande tidsstatistik för denna körning:

Kom ihåg att den här funktionen inte resulterar i sortering när du begär data sorterad efter n; du får i princip samma plan oavsett om du begär den beställda datan eller inte. Vi kan tillskriva det mesta av den extra tiden i det här testet jämfört med det föregående till de 100 miljoner radlägesbaserade variabeltilldelningarna.

Den bäst presterande T-SQL-lösningen som använde en beständig bastabell och därför resulterade i vissa I/O-operationer, även om mycket få, var Paul Whites lösning implementerad i funktionen dbo.GetNums_SQLkiwi. Jag täckte denna lösning i del 4.

Här är Pauls kod för att skapa både columnstore-tabellen som används av funktionen och själva funktionen:

-- Helper columnstore tableDROP TABLE OM FINNS dbo.CS; -- 64K rader (tillräckligt för 4B rader när korsfogade) -- kolumn 1 är alltid noll -- kolumn 2 är (1...65536) SELECT -- skriv som heltal INTE NULL -- (allt är normaliserat till 64 bitar i kolumnlager/batch-läge i alla fall) n1 =ISNULL(CONVERT(heltal, 0), 0), n2 =ISNULL(CONVERT(heltal, N.rn), 0)INTO dbo.CSFROM ( SELECT rn =ROW_NUMBER() OVER (ORDER BY @@SPID) FRÅN master.dbo.spt_values ​​AS SV1 CROSS JOIN master.dbo.spt_values ​​AS SV2 BESTÄLLNING EFTER rn ASC OFFSET 0 RADER HÄMTA NÄSTA ENDAST 65536 RADER) SOM N; -- En enda komprimerad radgrupp på 65 536 rader SKAPA CLUSTERED COLUMNSTORE INDEX CCI PÅ dbo.CS WITH (MAXDOP =1);GO -- Funktionen CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi( @low bigint =1) RETURNS N bigint ASRETURNS .rn, n =@low - 1 + N.rn, op =@high + 1 - N.rn FROM ( VÄLJ -- Använd @@TRANCOUNT istället för @@SPID om du gillar alla dina frågor seriell rn =ROW_NUMBER() ÖVER (ORDER BY @@SPID ASC) FRÅN dbo.CS AS N1 JOIN dbo.CS AS N2 -- Batch mode hash cross join -- Heltal inte null datatyp undvik hash probe residual -- Detta är alltid 0 =0 ON N2. n1 =N1.n1 WHERE -- Försök att undvika SQRT på negativa tal och möjliggör förenkling -- till enkel konstant skanning om @low> @high (med bokstaver) -- Inga startfilter i batchläge @high>=@low -- Grovfilter:-- Begränsa varje sida av korskopplingen till SQRT(målantal rader) -- IIF undviker SQRT på negativa tal med parametrar OCH N1.n2 <=KONVERTERA(heltal, CEILING(SQRT(CONVERT(float, IIF(@hög>=@låg, @hög - @låg + 1, 0))))) OCH N2.n2 <=CONVERT(heltal, CEILING(SQRT(CONVERT(float, IIF(@high>=@low, @high - @low + 1, 0)) ))) ) SOM N WHERE -- Exakt filter:-- Batch-läge filtrera den begränsade korskopplingen till det exakta antalet rader som behövs -- Undviker att optimeraren introducerar en rad-läge Top med följande radläge beräkningsskalär @låg - 2 + N.rn <@high;GO

Låt oss först testa det utan beställning med aggregattekniken, vilket resulterar i en hel-batch-mode-plan:

VÄLJ MAX(n) AS mx FRÅN dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);

Jag fick följande tid- och I/O-statistik för denna körning:

Låt oss testa funktionen i ordning med hjälp av variabeltilldelningstekniken:

DEKLARE @n SOM STOR; VÄLJ @n =n FRÅN dbo.GetNums_SQLkiwi(1, 100000000) BESTÄLL EFTER n OPTION(MAXDOP 1);

Liksom med den tidigare lösningen undviker även denna lösning explicit sortering i planen, och får därför samma plan oavsett om du frågar efter beställd data eller inte. Men återigen, detta test medför en extra påföljd främst på grund av den variabeltilldelningsteknik som används här, vilket resulterar i att den variabla tilldelningsdelen i planen bearbetas i radläge.

Här är tiden och I/O-statistiken som jag fick för den här exekveringen:

CLR-lösningar

Både Kamil Kosno och Adam Machanic tillhandahöll först en enkel CLR-only-lösning och kom senare med en mer sofistikerad CLR+T-SQL-kombo. Jag börjar med Kamils ​​lösningar och täcker sedan Adams lösningar.

Lösningar av Kamil Kosno

Här är CLR-koden som används i Kamils ​​första lösning för att definiera en funktion som heter GetNums_KamilKosno1:

använder System;använder System.Data.SqlTypes;using System.Collections;public partial class GetNumsKamil1{ [Microsoft.SqlServer.Server.SqlFunction(FillRowMethodName ="GetNums_KamilKosno1_Fill"), TableDefinition_Kanomil_Kannumer ="GetNums_KamilKosno1_Fill" (SqlInt64 låg, SqlInt64 hög) { return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0) :new GetNumsCS(low.Value, high.Value); } public static void GetNums_KamilKosno1_Fill(Object o, out SqlInt64 n) { n =(long)o; } privatklass GetNumsCS :IEnumerator { public GetNumsCS(long from, long to) { _lowrange =from; _current =_lågområde - 1; _highrange =till; } public bool MoveNext() { _current +=1; if (_current> _highrange) returnerar falskt; annars returneras sant; } public object Current { get { return _current; } } public void Reset() { _current =_lowrange - 1; } long _lowrange; lång _ström; lång _highrange; }}

Funktionen accepterar två ingångar som kallas låg och hög och returnerar en tabell med en BIGINT-kolumn som heter n. Funktionen är en strömmande typ, returnerar en rad med nästa nummer i serien per rad begäran från den anropande frågan. Som du kan se valde Kamil den mer formaliserade metoden för att implementera IEnumerator-gränssnittet, vilket innebär att implementera metoderna MoveNext (avancerar räknaren för att få nästa rad), Current (får raden i den aktuella uppräkningspositionen) och Återställ (ställer in räknaren till dess ursprungliga position, som är före den första raden).

Variabeln som innehåller det aktuella numret i serien kallas _current. Konstruktorn ställer in _current till den nedre gränsen för det begärda intervallet minus 1, och detsamma gäller för metoden Reset. MoveNext-metoden ökar _current med 1. Sedan, om _current är större än den höga gränsen för det begärda intervallet, returnerar metoden false, vilket betyder att den inte kommer att anropas igen. Annars återgår det sant, vilket betyder att det kommer att anropas igen. Metoden Current returnerar naturligtvis _current. Som du kan se, ganska grundläggande logik.

Jag kallade Visual Studio-projektet GetNumsKamil1 och använde sökvägen C:\Temp\ för det. Här är koden jag använde för att distribuera funktionen i testdb-databasen:

DROPPFUNKTION OM FINNS dbo.GetNums_KamilKosno1; SLUTA MONTERING OM FINNS GetNumsKamil1;GO SKAPA ENHET GetNumsKamil1 FRÅN 'C:\Temp\GetNumsKamil1\GetNumsKamil1\bin\Debug\GetNumsKamil1.dll';GO SKAPA FUNKTION @GetNumsKamil1.dll'; TABELL(n BIGINT) ORDER(n) SOM EXTERNT NAMN GetNumsKamil1.GetNumsKamil1.GetNums_KamilKosno1;GO

Lägg märke till användningen av ORDER-satsen i CREATE FUNCTION-satsen. Funktionen skickar ut raderna i n-ordning, så när raderna behöver tas in i planen i n-ordning, baserat på denna klausul vet SQL Server att den kan undvika en sortering i planen.

Låt oss testa funktionen, först med aggregattekniken, när beställning inte behövs:

VÄLJ MAX(n) AS mx FRÅN dbo.GetNums_KamilKosno1(1, 100000000);

Jag fick planen som visas i figur 1.

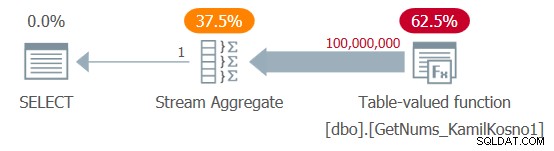Figur 1:Plan för dbo.GetNums_KamilKosno1-funktionen

Det finns inte mycket att säga om den här planen, förutom det faktum att alla operatörer använder radexekveringsläge.

Jag fick följande tidsstatistik för denna körning:

Och naturligtvis var inga logiska läsningar inblandade.

Låt oss testa funktionen i ordning med hjälp av variabeltilldelningstekniken:

DEKLARE @n SOM STOR; VÄLJ @n =n FRÅN dbo.GetNums_KamilKosno1(1, 100000000) BESTÄLL EFTER n;

Jag fick planen som visas i figur 2 för det här utförandet.

Figur 2:Planera för dbo.GetNums_KamilKosno1-funktionen med ORDER BY

Observera att det inte finns någon sortering i planen eftersom funktionen skapades med ORDER(n)-satsen. Det finns dock en viss ansträngning för att säkerställa att raderna verkligen sänds ut från funktionen i den utlovade ordningen. Detta görs med operatorerna Segment och Sequence Project, som används för att beräkna radnummer, och Assert-operatorn, som avbryter exekveringen av frågan om testet misslyckas. Det här arbetet har linjär skalning - till skillnad från n log n-skalningen du skulle ha fått om en sorts krävdes - men det är fortfarande inte billigt. Jag fick följande tidsstatistik för detta test:

Resultaten kan vara överraskande för vissa – särskilt de som intuitivt antog att de CLR-baserade lösningarna skulle prestera bättre än T-SQL. Som du kan se är exekveringstiderna en storleksordning längre än med vår bäst presterande T-SQL-lösning.

Kamils ​​andra lösning är en CLR-T-SQL hybrid. Utöver de låga och höga ingångarna, lägger CLR-funktionen (GetNums_KamilKosno2) till en steginmatning och returnerar värden mellan låg och hög som är steg ifrån varandra. Här är CLR-koden som Kamil använde i sin andra lösning:

using System;using System.Data.SqlTypes;using System.Collections; public partial class GetNumsKamil2{ [Microsoft.SqlServer.Server.SqlFunction(DataAccess =Microsoft.SqlServer.Server.DataAccessKind.None, IsDeterministic =true, IsPrecise =true, FillRowMethodName ="GetNums_Fill") ="GetNums_Fill"), "static BIGDefinition]", Tnic IEnumerator GetNums_KamilKosno2(SqlInt64 låg, SqlInt64 hög, SqlInt64 steg) { return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0, step.Value) :new GetNumsCS(low.Value, high.Value, step.Value); } public static void GetNums_Fill(Object o, out SqlInt64 n) { n =(long)o; } privat klass GetNumsCS :IEnumerator { public GetNumsCS(long from, long to, long step) { _lowrange =from; _steg =steg; _current =_lågområde - _steg; _highrange =till; } public bool MoveNext() { _current =_current + _step; if (_current> _highrange) returnerar falskt; annars returneras sant; } public object Current { get { return _current; } } public void Reset() { _current =_lowrange - _step; } long _lowrange; lång _ström; lång _highrange; långt _steg; }}

Jag döpte VS-projektet GetNumsKamil2, placerade det i sökvägen C:\Temp\ också och använde följande kod för att distribuera det i testdb-databasen:

-- Skapa sammansättning och funktionDROP-FUNKTION OM FINNS dbo.GetNums_KamilKosno2;DROP ASSEMBLY IF EXISTS GetNumsKamil2;GO SKAPA ASSEMBLY GetNumsKamil2 FRÅN 'C:\Temp\GetNumsKamil2\GetNumGO\GetNumGO\C:\Temp\GetNumsKamil2\GetNumGO\DebugNums\GetNumGOc\DLL\GetNumsKamil2\GetNumG. .GetNums_KamilKosno2 (@low AS BIGINT =1, @high AS BIGINT, @step AS BIGINT) RETURNERAR TABELL(n BIGINT) ORDER(n) SOM EXTERNT NAMN GetNumsKamil2.GetNumsKamil2.GetNums_GOmilKosno2; 

 Som ett exempel för att använda funktionen, här är en begäran om att generera värden mellan 5 och 59, med ett steg på 10:
 
VÄLJ n FRÅN dbo.GetNums_KamilKosno2(5, 59, 10);
 

 Denna kod genererar följande utdata:
 
n---51525354555
 

 När det gäller T-SQL-delen använde Kamil en funktion som heter dbo.GetNums_Hybrid_Kamil2, med följande kod:
 
SKAPA ELLER ÄNDRA FUNKTION dbo.GetNums_Hybrid_Kamil2(@low AS BIGINT, @high AS BIGINT) RETURER TABLEASRETURN SELECT TOPP (@high - @low + 1) V.n FRÅN dbo.GetNums_KamilKosno2(@GN 1) AS KORSA TILLÄMPNING (VÄRDEN(0+GN.n),(1+GN.n),(2+GN.n),(3+GN.n),(4+GN.n), (5+GN.n) ),(6+GN.n),(7+GN.n),(8+GN.n),(9+GN.n)) AS V(n);GO
 

 Som du kan se, anropar T-SQL-funktionen CLR-funktionen med samma @låg och @hög ingångar som den får, och använder i detta exempel en stegstorlek på 10. Frågan använder CROSS APPLY mellan CLR-funktionens resultat och en tabell -värde-konstruktor som genererar de slutliga talen genom att lägga till värden i intervallet 0 till 9 till början av steget. TOP-filtret används för att säkerställa att du inte får fler än det antal nummer du begärt. 
 

 Viktigt: Jag bör betona att Kamil här gör ett antagande om att TOP-filtret tillämpas baserat på resultatnummerordningen, vilket inte är riktigt garanterat eftersom frågan inte har en ORDER BY-sats. Om du antingen lägger till en ORDER BY-sats för att stödja TOP, eller ersätter TOP med ett WHERE-filter, för att garantera ett deterministiskt filter, kan detta helt förändra lösningens prestandaprofil.
 

 Låt oss i alla fall först testa funktionen utan ordning med aggregattekniken:
 
VÄLJ MAX(n) AS mx FROM dbo.GetNums_Hybrid_Kamil2(1, 100000000);
 

 Jag fick planen som visas i figur 3 för det här utförandet.
 

 Figur 3:Plan för dbo.GetNums_Hybrid_Kamil2-funktionen 
 

 Återigen använder alla operatorer i planen radexekveringsläge.
 

 Jag fick följande tidsstatistik för denna körning:
 CPU-tid =13985 ms, förfluten tid =14069 ms . 

 Och naturligtvis inga logiska läsningar.
 

 Låt oss testa funktionen med ordning:
 
DEKLARE @n SOM STOR; VÄLJ @n =n FRÅN dbo.GetNums_Hybrid_Kamil2(1, 100000000) BESTÄLL EFTER n;
 

 Jag fick planen som visas i figur 4.
 

 Figur 4:Planera för dbo.GetNums_Hybrid_Kamil2-funktionen med ORDER BY 
 

 Eftersom resultatsiffrorna är resultatet av manipulering av den nedre gränsen för steget som returneras av CLR-funktionen och deltat som lagts till i tabellvärdekonstruktorn, litar optimeraren inte på att resultatnumren genereras i den begärda ordningen, och lägger till explicit sortering i planen.
 

 Jag fick följande tidsstatistik för denna körning:
 CPU-tid =68703 ms, förfluten tid =84538 ms . 

 Så det verkar som att när ingen beställning behövs, fungerar Kamils ​​andra lösning bättre än hans första. Men när ordning behövs är det tvärtom. Hur som helst är T-SQL-lösningarna snabbare. Personligen skulle jag lita på riktigheten av den första lösningen, men inte den andra.
 
Lösningar av Adam Machanic
 

 Adams första lösning är också en grundläggande CLR-funktion som hela tiden ökar en räknare. Bara istället för att använda det mer involverade formaliserade tillvägagångssättet som Kamil gjorde, använde Adam ett enklare tillvägagångssätt som anropar avkastningskommandot per rad som måste returneras.
 

 Här är Adams CLR-kod för hans första lösning, som definierar en streamingfunktion som heter GetNums_AdamMachanic1:
 
använda System.Data.SqlTypes;använda System.Collections; public partial class GetNumsAdam1{ [Microsoft.SqlServer.Server.SqlFunction( FillRowMethodName ="GetNums_AdamMachanic1_fill", TableDefinition ="n BIGINT")] public static IEnumerable GetNums_AdamMachanic1(SqlInt.)In {4min_max.Vint. var max_int =max.Value; for (; min_int <=max_int; min_int++) { yield return (min_int); } } offentligt statiskt tomrum GetNums_AdamMachanic1_fill(objekt o, ut långt i) { i =(långt)o; }};
 

 Lösningen är så elegant i sin enkelhet. Som du kan se accepterar funktionen två ingångar som kallas min och max som representerar de låga och höga gränspunkterna för det begärda området och returnerar en tabell med en BIGINT-kolumn som heter n. Funktionen initierar variabler som kallas min_int och max_int med respektive funktions indataparametervärden. Funktionen kör sedan en slinga så lång som min_int <=max_int, som i varje iteration ger en rad med det aktuella värdet på min_int och ökar min_int med 1. Det är allt.
 

 Jag döpte projektet till GetNumsAdam1 i VS, placerade det i C:\Temp\ och använde följande kod för att distribuera det:
 
-- Skapa sammansättning och funktionDROP-FUNKTION OM FINNS dbo.GetNums_AdamMachanic1;DROP ASSEMBLY IF EXISTS GetNumsAdam1;GO SKAPA ASSEMBLY GetNumsAdam1 FRÅN 'C:\Temp\GetNumsAdam1\GetNumGOgNumGOgNumgNumGoDllcFunC:\Temp\GetNumsAdam1\GetNumGOgNumGOgNumgNumgO .GetNums_AdamMachanic1(@low AS BIGINT =1, @high AS BIGINT) RETURTABELL(n BIGINT) ORDER(n) SOM EXTERNT NAMN GetNumsAdam1.GetNumsAdam1.GetNums_AdamMachanic1;GO
 

 Jag använde följande kod för att testa den med aggregattekniken, för fall då ordning inte spelar någon roll:
 
VÄLJ MAX(n) AS mx FRÅN dbo.GetNums_AdamMachanic1(1, 100000000);
 

 Jag fick planen som visas i figur 5 för det här utförandet.
 

 Figur 5:Plan för dbo.GetNums_AdamMachanic1-funktionen 
 

 Planen är mycket lik planen du såg tidigare för Kamils ​​första lösning, och detsamma gäller dess prestanda. Jag fick följande tidsstatistik för denna körning:
 CPU-tid =36687 ms, förfluten tid =36952 ms . 

 Och naturligtvis behövdes inga logiska läsningar.
 

 Låt oss testa funktionen i ordning med hjälp av variabeltilldelningstekniken:
 
DEKLARE @n SOM STOR; VÄLJ @n =n FRÅN dbo.GetNums_AdamMachanic1(1, 100000000) BESTÄLL EFTER n;
 

 Jag fick planen som visas i figur 6 för det här utförandet.
 

 Figur 6:Planera för dbo.GetNums_AdamMachanic1-funktionen med ORDER BY 
 

 Återigen ser planen ut som den du såg tidigare för Kamils ​​första lösning. Det fanns inget behov av explicit sortering eftersom funktionen skapades med ORDER-klausulen, men planen inkluderar en del arbete för att verifiera att raderna verkligen returneras ordnade som utlovat.
 

 Jag fick följande tidsstatistik för denna körning:
 CPU-tid =55047 ms, förfluten tid =55498 ms . 

 I sin andra lösning kombinerade Adam även en CLR-del och en T-SQL-del. Här är Adams beskrivning av logiken han använde i sin lösning:
 "Jag försökte tänka på hur jag skulle kunna lösa problemet med SQLCLR-chattilighet, och även den centrala utmaningen med denna nummergenerator i T-SQL, vilket är det faktum att vi inte bara kan magiska rader till existens.
 

 CLR är ett bra svar för den andra delen men försvåras förstås av det första numret. Så som en kompromiss skapade jag en T-SQL TVF [kallad GetNums_AdamMachanic2_8192] hårdkodad med värdena 1 till 8192. (Ganska godtyckligt val, men för stort och QO börjar kvävas lite av det.) Därefter modifierade jag min CLR-funktion [ namngett GetNums_AdamMachanic2_8192_base] för att mata ut två kolumner, "max_base" och "base_add", och hade det utmatningsrader som:
 
 
max_bas, base_add
——————
8191, 1
8192, 8192
8192, 16384
…
8192, 99991552
257, 99999744
 

 Nu är det en enkel slinga. CLR-utgången skickas till T-SQL TVF, som är inställd för att endast återgå till "max_base"-rader i dess hårdkodade uppsättning. Och för varje rad lägger den till "base_add" till värdet, och genererar därmed de nödvändiga siffrorna. Nyckeln här, tror jag, är att vi kan generera N rader med endast en enda logisk korskoppling, och CLR-funktionen behöver bara returnera 1/8192 lika många rader, så den är tillräckligt snabb för att fungera som basgenerator." 

 Logiken verkar ganska okomplicerad.
 

 Här är koden som används för att definiera CLR-funktionen som heter GetNums_AdamMachanic2_8192_base:
 
använda System.Data.SqlTypes;använda System.Collections; public partial class GetNumsAdam2{ private struct row { public long max_base; public long base_add; } [Microsoft.SqlServer.Server.SqlFunction( FillRowMethodName ="GetNums_AdamMachanic2_8192_base_fill", TableDefinition ="max_base int, base_add int")] public static IEnumerable GetNums_AdamMachanic2_q4Smax.I minal var max_int =max.Value; var min_group =min_int / 8192; var max_group =max_int / 8192; för (; min_grupp <=max_grupp; min_grupp++) { if (min_int> max_int) avkastningsbrytning; var max_base =8192 - (min_int % 8192); if (min_grupp ==max_grupp &&max_int <(((max_int / 8192) + 1) * 8192) - 1) max_base =max_int - min_int + 1; yield return (ny rad() { max_base =max_base, base_add =min_int } ); min_int =(min_grupp + 1) * 8192; } } public static void GetNums_AdamMachanic2_8192_base_fill(objekt o, ut lång max_bas, ut lång bas_add) { var r =(rad)o; max_bas =r.max_base; base_add =r.base_add; }};
 

 Jag döpte VS-projektet till GetNumsAdam2 och placerade i sökvägen C:\Temp\ som med de andra projekten. Här är koden jag använde för att distribuera funktionen i testdb-databasen:
 
-- Skapa assembly och functionDROP FUNCTION IF EXISTS dbo.GetNums_AdamMachanic2_8192_base;DROPP ASSEMBLY IF EXISTS GetNumsAdam2;GO CREATE ASSEMBLY GetNumsAdam2 FRÅN 'C:\Temp\GetNumsAdamsAdamC:\Temp\GetNumsAdamC:\Temp\GetNumsAdam C:\Temp\GetNumsAdamC:\Temp\GetNumsAdam'DLL\GetNumsAdam C:\Temp\GetNumsAdamc .GetNums_AdamMachanic2_8192_base(@max_base AS BIGINT, @add_base AS BIGINT) RETURTABELL(max_base BIGINT, base_add BIGINT) BESTÄLLNING(base_add) SOM EXTERNT NAMN GetNumsAdam2.GetNum_2.GetNum_2.GetNums2.GetNums2.GetNumgO 

 Här är ett exempel på hur du använder GetNums_AdamMachanic2_8192_base med intervallet 1 till 100M:
 
VÄLJ * FRÅN dbo.GetNums_AdamMachanic2_8192_base(1, 100000000);
 

 Denna kod genererar följande utdata, som visas här i förkortad form:
 
max_base base_add ------------------------------------8191 18192 81928192 163848192 245768192 32768...8192 999669768192 999751688192 999833608192 99991552257 99999744(12208 rader påverkade)
 

 Här är koden med definitionen av T-SQL-funktionen GetNums_AdamMachanic2_8192 (förkortad):
 
SKAPA ELLER ÄNDRA FUNKTION dbo.GetNums_AdamMachanic2_8192(@max_base AS BIGINT, @add_base AS BIGINT) RETUR TABLEASRETURN SELECT TOPP (@max_base) V.i + @add_base AS val FROM ( VALUES ), (0), (3), (4), ... (8187), (8188), (8189), (8190), (8191) ) AS V(i);GO
 

 Viktigt: Även här bör jag betona att i likhet med vad jag sa om Kamils ​​andra lösning, gör Adam här ett antagande att TOP-filtret kommer att extrahera de översta raderna baserat på radens utseendeordning i tabellvärdeskonstruktorn, vilket inte är riktigt garanterat. Om du lägger till en ORDER BY-sats för att stödja TOP eller ändrar filtret till ett WHERE-filter får du ett deterministiskt filter, men detta kan helt ändra lösningens prestandaprofil. 
 

 Slutligen, här är den yttersta T-SQL-funktionen, dbo.GetNums_AdamMachanic2, som slutanvändaren anropar för att få nummerserien:
 
SKAPA ELLER ÄNDRA FUNKTION dbo.GetNums_AdamMachanic2(@low AS BIGINT =1, @high AS BIGINT) RETURER TABLEASRETURN VÄLJ Y.val AS n FROM ( SELECT max_base, base_add FROM dbo.GetNums_AdamMachanic @baseMachanic) . X CROSS APPLY dbo.GetNums_AdamMachanic2_8192(X.max_base, X.base_add) AS YGO
 

 Den här funktionen använder operatorn CROSS APPLY för att tillämpa den inre T-SQL-funktionen dbo.GetNums_AdamMachanic2_8192 per rad som returneras av den inre CLR-funktionen dbo.GetNums_AdamMachanic2_8192_base.
 

 Låt oss först testa den här lösningen med aggregattekniken när ordning inte spelar någon roll:
 
VÄLJ MAX(n) AS mx FRÅN dbo.GetNums_AdamMachanic2(1, 100000000);
 

 Jag fick planen som visas i figur 7 för det här utförandet.
 

 Figur 7:Plan för dbo.GetNums_AdamMachanic2-funktionen 
 

 Jag fick följande tidsstatistik för detta test:
 SQL Server analys och kompileringstid :CPU-tid =313 ms, förfluten tid =339 ms .
SQL Server exekveringstid :CPU-tid =8859 ms, förfluten tid =8849 ms . 

 Inga logiska läsningar behövdes.
 

 Exekveringstiden är inte dålig, men lägg märke till den höga kompileringstiden på grund av den stora tabellvärdekonstruktorn som används. Du skulle betala så lång kompileringstid oavsett intervallstorleken som du begär, så detta är särskilt knepigt när du använder funktionen med mycket små intervall. Och den här lösningen är fortfarande långsammare än T-SQL. 
 

 Låt oss testa funktionen med ordning:
 
DEKLARE @n SOM STOR; VÄLJ @n =n FRÅN dbo.GetNums_AdamMachanic2(1, 100000000) BESTÄLL AV n;
 

 Jag fick planen som visas i figur 8 för det här utförandet.
 

 Figur 8:Planera för dbo.GetNums_AdamMachanic2-funktionen med ORDER BY 
 

 Precis som med Kamils ​​andra lösning behövs en explicit sortering i planen, vilket innebär en betydande prestationsstraff. Här är tidsstatistiken som jag fick för det här testet:
 Utförandetid:CPU-tid =54891 ms, förfluten tid =60981 ms . 

 Dessutom finns det fortfarande den höga kompileringstiden på ungefär en tredjedels sekund. 
 
Slutsats
 

 Det var intressant att testa CLR-baserade lösningar på nummerserieutmaningen eftersom många från början antog att den bäst presterande lösningen sannolikt kommer att vara en CLR-baserad. Kamil och Adam använde liknande metoder, med det första försöket med en enkel loop som ökar en räknare och ger en rad med nästa värde per iteration, och det mer sofistikerade andra försöket som kombinerar CLR- och T-SQL-delar. Personligen känner jag mig inte bekväm med det faktum att de i både Kamils ​​och Adams andra lösningar förlitade sig på ett icke-deterministiskt TOP-filter, och när jag konverterade det till ett deterministiskt i min egen testning, hade det en negativ inverkan på lösningens prestanda. . Hur som helst, våra två T-SQL-lösningar presterar bättre än CLR-lösningarna och resulterar inte i explicit sortering i planen när du behöver raderna beställda. Så jag ser inte riktigt värdet i att fortsätta CLR-rutten längre. Figur 9 har en prestandasammanfattning av lösningarna som jag presenterade i den här artikeln.
 

 Figur 9:Jämförelse av tidsprestanda 
 

 För mig borde GetNums_AlanCharlieItzikBatch vara den bästa lösningen när du absolut inte behöver något I/O-fotavtryck, och GetNums_SQKWiki bör föredras när du inte har något emot ett litet I/O-fotavtryck. Naturligtvis kan vi alltid hoppas att Microsoft en dag lägger till detta kritiskt användbara verktyg som ett inbyggt, och förhoppningsvis om/när de gör det, kommer det att vara en prestandalösning som stöder batchbearbetning och parallellitet. Så glöm inte att rösta på denna begäran om funktionsförbättring, och kanske till och med lägg till dina kommentarer om varför det är viktigt för dig.
 

 Jag gillade verkligen att arbeta med den här serien. Jag lärde mig mycket under processen och hoppas att du också gjorde det.