Den här artikeln visar hur SQL Server kombinerar densitetsinformation från statistik med flera enkolumner för att skapa en kardinalitetsuppskattning för en aggregering över flera kolumner. Detaljerna är förhoppningsvis intressanta i sig. De ger också en inblick i några av de allmänna tillvägagångssätt och algoritmer som används av kardinalitetsskattaren.
Tänk på följande AdventureWorks-exempeldatabasfråga, som listar antalet produktlagerartiklar i varje fack på varje hylla i lagret:
SELECT
INV.Shelf,
INV.Bin,
COUNT_BIG(*)
FROM Production.ProductInventory AS INV
GROUP BY
INV.Shelf,
INV.Bin
ORDER BY
INV.Shelf,
INV.Bin;
Den beräknade exekveringsplanen visar 1 069 rader som läses från tabellen, sorterade i Shelf och Bin ordning och sedan aggregerad med en Stream Aggregate-operator:
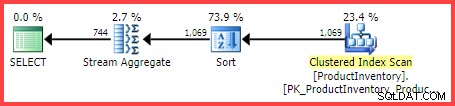
Uppskattad exekveringsplan
Frågan är hur kom SQL Server-frågeoptimeraren fram till den slutliga uppskattningen på 744 rader?
Tillgänglig statistik
När du kompilerar frågan ovan kommer frågeoptimeraren att skapa statistik i en kolumn på Shelf och Bin kolumner, om lämplig statistik inte redan finns. Denna statistik ger bland annat information om antalet distinkta kolumnvärden (i densitetsvektorn):
DBCC SHOW_STATISTICS
(
[Production.ProductInventory],
[Shelf]
)
WITH DENSITY_VECTOR;
DBCC SHOW_STATISTICS
(
[Production.ProductInventory],
[Bin]
)
WITH DENSITY_VECTOR; Resultaten sammanfattas i tabellen nedan (den tredje kolumnen är beräknad från densiteten):
| Kolumn | Täthet | 1 / Densitet |
|---|---|---|
| Hylla | 0,04761905 | 21 |
| Bin | 0,01612903 | 62 |
Vektorinformation om hyll- och papperstäthet
Som dokumentationen noterar är den reciproka densiteten antalet distinkta värden i kolumnen. Från statistikinformationen som visas ovan vet SQL Server att det fanns 21 distinkta Shelf värden och 62 distinkta Bin värden i tabellen, när statistiken samlades in.
Uppgiften att uppskatta antalet rader som produceras av en GROUP BY sats är trivial när endast en kolumn är inblandad (förutsatt att inga andra predikat). Det är till exempel lätt att se att GROUP BY Shelf kommer att producera 21 rader; GROUP BY Bin kommer att producera 62.
Det är dock inte omedelbart klart hur SQL Server kan uppskatta antalet distinkta (Shelf, Bin) kombinationer för vår GROUP BY Shelf, Bin fråga. För att ställa frågan på ett lite annorlunda sätt:Med tanke på 21 hyllor och 62 papperskorgar, hur många unika kombinationer av hyllor och papperskorgar kommer det att finnas? Om man bortser från fysiska aspekter och annan mänsklig kunskap om problemdomänen kan svaret vara allt från max(21, 62) =62 till (21 * 62) =1 302. Utan mer information finns det inget självklart sätt att veta var man ska lägga en uppskattning i det intervallet.
Ändå, för vår exempelfråga, uppskattar SQL Server 744.312 rader (avrundade till 744 i vyn Plan Explorer) men på vilken grund?
Kardinalitetsuppskattning utökad händelse
Det dokumenterade sättet att undersöka kardinalitetsuppskattningsprocessen är att använda den utökade händelsen query_optimizer_estimate_cardinality (trots att det är i "debug"-kanalen). Medan en session som samlar in den här händelsen körs, får operatörer för körningsplan en ytterligare egenskap StatsCollectionId som kopplar individuella operatörsuppskattningar till de beräkningar som producerade dem. För vår exempelfråga är statistikinsamlings-id 2 kopplat till kardinalitetsuppskattningen för gruppen efter aggregerad operator.
Relevant utdata från den utökade händelsen för vår testfråga är:
<data name="calculator">
<type name="xml" package="package0"></type>
<value>
<CalculatorList>
<DistinctCountCalculator CalculatorName="CDVCPlanLeaf" SingleColumnStat="Shelf,Bin" />
</CalculatorList>
</value>
</data>
<data name="stats_collection">
<type name="xml" package="package0"></type>
<value>
<StatsCollection Name="CStCollGroupBy" Id="2" Card="744.31">
<LoadedStats>
<StatsInfo DbId="6" ObjectId="258099960" StatsId="3" />
<StatsInfo DbId="6" ObjectId="258099960" StatsId="4" />
</LoadedStats>
</StatsCollection>
</value>
</data> Det finns en del användbar information där, helt klart.
Vi kan se att kalkylatorklassen för planblads distinkta värden (CDVCPlanLeaf ) användes med en kolumnstatistik på Shelf och Bin som ingångar. Statistikinsamlingselementet matchar detta fragment med id (2) som visas i exekveringsplanen, som visar kardinalitetsuppskattningen på 744.31 , och mer information om de statistiska objekt-ID som används också.
Tyvärr finns det inget i händelseutdata som säger exakt hur räknaren kom fram till den slutliga siffran, vilket är det vi verkligen är intresserade av.
Kombinerar distinkta siffror
Om vi går en mindre dokumenterad väg kan vi begära en uppskattad plan för frågan med spårningsflaggor 2363 och 3604 aktiverade:
SELECT
INV.Shelf,
INV.Bin,
COUNT_BIG(*)
FROM Production.ProductInventory AS INV
GROUP BY
INV.Shelf,
INV.Bin
ORDER BY
INV.Shelf,
INV.Bin
OPTION (QUERYTRACEON 3604, QUERYTRACEON 2363); Detta returnerar felsökningsinformation till fliken Meddelanden i SQL Server Management Studio. Den intressanta delen återges nedan:
Begin distinct values computation
Input tree:
LogOp_GbAgg OUT(QCOL: [INV].Shelf,QCOL: [INV].Bin,COL: Expr1001 ,) BY(QCOL: [INV].Shelf,QCOL: [INV].Bin,)
CStCollBaseTable(ID=1, CARD=1069 TBL: Production.ProductInventory AS TBL: INV)
AncOp_PrjList
AncOp_PrjEl COL: Expr1001
ScaOp_AggFunc stopCountBig
ScaOp_Const TI(int,ML=4) XVAR(int,Not Owned,Value=0)
Plan for computation:
CDVCPlanLeaf
0 Multi-Column Stats, 2 Single-Column Stats, 0 Guesses
Loaded histogram for column QCOL: [INV].Shelf from stats with id 3
Loaded histogram for column QCOL: [INV].Bin from stats with id 4
Using ambient cardinality 1069 to combine distinct counts:
21
62
Combined distinct count: 744.312
Result of computation: 744.312
Stats collection generated:
CStCollGroupBy(ID=2, CARD=744.312)
CStCollBaseTable(ID=1, CARD=1069 TBL: Production.ProductInventory AS TBL: INV)
End distinct values computation Detta visar ungefär samma information som det utökade evenemanget gjorde i ett (förmodligen) lättare att konsumera format:
- Indatarelationsoperatorn för att beräkna en kardinalitetsuppskattning för (
LogOp_GbAgg– logisk grupp efter aggregat) - Den använda räknaren (
CDVCPlanLeaf) och inmatningsstatistik - De resulterande statistikinsamlingsdetaljerna
Den intressanta nya informationen är delen om att använda omgivande kardinalitet för att kombinera distinkta siffror .
Detta visar tydligt att värdena 21, 62 och 1069 användes, men (frustrerande) fortfarande inte exakt vilka beräkningar som gjordes för att komma fram till 744.312 resultat.
Till felsökaren!
Genom att bifoga en debugger och använda offentliga symboler kan vi i detalj utforska kodsökvägen som följs under kompileringen av exempelfrågan.
Översiktsbilden nedan visar den övre delen av anropsstacken vid en representativ punkt i processen:
MSVCR120!log sqllang!OdblNHlogN sqllang!CCardUtilSQL12::ProbSampleWithoutReplacement sqllang!CCardUtilSQL12::CardDistinctMunged sqllang!CCardUtilSQL12::CardDistinctCombined sqllang!CStCollAbstractLeaf::CardDistinctImpl sqllang!IStatsCollection::CardDistinct sqllang!CCardUtilSQL12::CardGroupByHelperCore sqllang!CCardUtilSQL12::PstcollGroupByHelper sqllang!CLogOp_GbAgg::PstcollDeriveCardinality sqllang!CCardFrameworkSQL12::DeriveCardinalityProperties
Det finns några intressanta detaljer här. När vi arbetar nerifrån och upp ser vi att kardinalitet härleds med den uppdaterade CE (CCardFrameworkSQL12 ) tillgänglig i SQL Server 2014 och senare (original CE är CCardFrameworkSQL7 ), för gruppen efter aggregerad logisk operator (CLogOp_GbAgg ).
Att beräkna den distinkta kardinaliteten innebär att kombinera (munging) flera ingångar, med hjälp av sampling utan ersättning.
Referensen till H och en (naturlig) logaritm i den andra metoden från toppen visar användningen av Shannon Entropy i beräkningen:
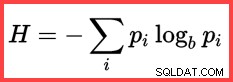
Shannon Entropy
Entropi kan användas för att uppskatta informationskorrelationen (ömsesidig information) mellan två statistik:
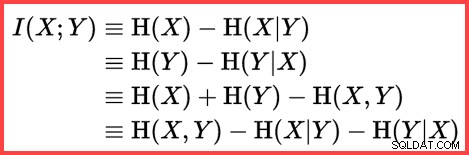
Ömsesidig information
Genom att sammanställa allt detta kan vi konstruera ett T-SQL-beräkningsskript som matchar hur SQL Server använder sampling utan ersättning, Shannon Entropy och ömsesidig information för att producera den slutliga kardinalitetsuppskattningen.
Vi börjar med inmatningstalen (omgivande kardinalitet och antalet distinkta värden i varje kolumn):
DECLARE
@Card float = 1069,
@Distinct1 float = 21,
@Distinct2 float = 62; frekvensen för varje kolumn är det genomsnittliga antalet rader per distinkt värde:
DECLARE
@Frequency1 float = @Card / @Distinct1,
@Frequency2 float = @Card / @Distinct2; Sampling utan ersättning (SWR) är en enkel fråga om att subtrahera det genomsnittliga antalet rader per distinkt värde (frekvens) från det totala antalet rader:
DECLARE
@SWR1 float = @Card - @Frequency1,
@SWR2 float = @Card - @Frequency2,
@SWR3 float = @Card - @Frequency1 - @Frequency2; Beräkna entropierna (N log N) och ömsesidig information:
DECLARE
@E1 float = (@SWR1 + 0.5) * LOG(@SWR1),
@E2 float = (@SWR2 + 0.5) * LOG(@SWR2),
@E3 float = (@SWR3 + 0.5) * LOG(@SWR3),
@E4 float = (@Card + 0.5) * LOG(@Card);
-- Using logarithms allows us to express
-- multiplication as addition and division as subtraction
DECLARE
@MI float = EXP(@E1 + @E2 - @E3 - @E4); Nu har vi uppskattat hur korrelerade de två uppsättningarna statistik är, vi kan beräkna den slutliga uppskattningen:
SELECT (1e0 - @MI) * @Distinct1 * @Distinct2;
Resultatet av beräkningen är 744.311823994677, vilket är 744.312 avrundat till tre decimaler.
För enkelhetens skull, här är hela koden i ett block:
DECLARE
@Card float = 1069,
@Distinct1 float = 21,
@Distinct2 float = 62;
DECLARE
@Frequency1 float = @Card / @Distinct1,
@Frequency2 float = @Card / @Distinct2;
-- Sample without replacement
DECLARE
@SWR1 float = @Card - @Frequency1,
@SWR2 float = @Card - @Frequency2,
@SWR3 float = @Card - @Frequency1 - @Frequency2;
-- Entropy
DECLARE
@E1 float = (@SWR1 + 0.5) * LOG(@SWR1),
@E2 float = (@SWR2 + 0.5) * LOG(@SWR2),
@E3 float = (@SWR3 + 0.5) * LOG(@SWR3),
@E4 float = (@Card + 0.5) * LOG(@Card);
-- Mutual information
DECLARE
@MI float = EXP(@E1 + @E2 - @E3 - @E4);
-- Final estimate
SELECT (1e0 - @MI) * @Distinct1 * @Distinct2; Sluta tankar
Den slutliga uppskattningen är ofullkomlig i det här fallet – exempelfrågan returnerar faktiskt 441 rader.
För att få en förbättrad uppskattning kan vi förse optimeraren med bättre information om densiteten för Bin och Shelf kolumner med hjälp av statistik med flera kolumner. Till exempel:
CREATE STATISTICS stat_Shelf_Bin ON Production.ProductInventory (Shelf, Bin);
Med den statistiken på plats (antingen som given, eller som en bieffekt av att lägga till ett liknande flerkolumnindex), är kardinalitetsuppskattningen för exempelfrågan helt rätt. Det är dock sällsynt att beräkna en så enkel aggregering. Med ytterligare predikat kan flerkolumnstatistiken vara mindre effektiv. Ändå är det viktigt att komma ihåg att den ytterligare densitetsinformation som tillhandahålls av statistik med flera kolumner kan vara användbar för aggregering (liksom jämställdhetsjämförelser).
Utan statistik med flera kolumner kan en aggregerad fråga med ytterligare predikat fortfarande använda den väsentliga logiken som visas i den här artikeln. Till exempel, istället för att tillämpa formeln på tabellens kardinalitet, kan den användas för att mata in histogram steg för steg.
Relaterat innehåll:Kardinalitetsuppskattning för ett predikat på ett COUNT-uttryck
