Den här artikeln är den andra i en serie om optimeringströsklar relaterade till gruppering och aggregering av data. I del 1 gav jag den omvända formeln för Stream Aggregate-operatörskostnaden. Jag förklarade att den här operatören måste konsumera raderna ordnade av grupperingsuppsättningen (valfri ordning av dess medlemmar), och att när data erhålls förbeställda från ett index får du linjär skalning med avseende på antalet rader och antalet grupper. Dessutom behövs inget minnesanslag i ett sådant fall.
I den här artikeln fokuserar jag på kostnadsberäkning och skalning av en strömaggregatbaserad operation när data inte erhålls förbeställd från ett index, utan måste sorteras först.
I mina exempel kommer jag att använda PerformanceV3-exempeldatabasen, som i del 1. Du kan ladda ner skriptet som skapar och fyller denna databas härifrån. Innan du kör exemplen från den här artikeln, se till att du kör följande kod först för att släppa ett par onödiga index:
DROP INDEX idx_nc_sid_od_cid ON dbo.Orders;DROP INDEX idx_unc_od_oid_i_cid_eid ON dbo.Orders;
De enda två indexen som bör finnas kvar i den här tabellen är idx_cl_od (klustrade med orderdate som nyckel) och PK_Orders (icke-klustrad med orderid som nyckel).
Sortera + Stream Aggregate
Fokus i den här artikeln är att försöka ta reda på hur en strömaggregatsoperation skalas när data inte är förbeställda av grupperingsuppsättningen. Eftersom Stream Aggregate-operatören måste behandla de beställda raderna, om de inte är förbeställda i ett index, måste planen inkludera en explicit Sorteringsoperator. Så kostnaden för den aggregerade operationen som du bör ta i beräkningen är summan av kostnaderna för Sortera + Stream Aggregate-operatörerna.
Jag kommer att använda följande fråga (vi kallar den fråga 1) för att demonstrera en plan som involverar sådan optimering:
SELECT shipperid, MAX(orderdate) AS maxod FROM (SELECT TOP (100) * FROM dbo.Orders) AS D GROUP BY shipperid;
Planen för denna fråga visas i figur 1.

Figur 1:Plan för fråga 1
Anledningen till att jag använder ett tabelluttryck med ett TOP-filter är för att kontrollera det exakta antalet (uppskattade) rader som är involverade i grupperingen och aggregeringen. Genom att tillämpa kontrollerade ändringar blir det lättare att försöka omvända kostnadsformlerna.
Om du undrar varför filtrera ett så litet antal rader i det här exemplet, har det att göra med optimeringströskelvärdena som gör denna strategi att föredra framför Hash Aggregate-algoritmen. I del 3 kommer jag att beskriva kostnadsberäkningen och skalningen av hashalternativet. I de fall där optimeraren inte väljer en flödesaggregationsoperation själv, t.ex. när ett stort antal rader är inblandade, kan du alltid tvinga fram det med tipset OPTION(ORDER GROUP) under forskningsprocessen. När du fokuserar på kostnadsberäkningen av serieplaner kan du självklart lägga till en MAXDOP 1-tips för att eliminera parallellism.
Som nämnts, för att utvärdera kostnaden och skalningen av en icke-förbeställd strömaggregatalgoritm, måste du ta hänsyn till summan av operatörerna Sortera + Strömaggregat. Du känner redan till kostnadsformeln för Stream Aggregate-operatören från del 1:
@numrows * 0,0000006 + @numrows * 0,0000005I vår fråga har vi 100 uppskattade inmatningsrader och 5 uppskattade utdatagrupper (5 distinkta avsändar-ID:n uppskattade baserat på densitetsinformation). Så kostnaden för Stream Aggregate-operatören i vår plan är:
100 * 0,0000006 + 5 * 0,0000005 =0,0000625Låt oss försöka ta reda på kostnadsformeln för sorteringsoperatorn. Kom ihåg att vårt fokus är den uppskattade kostnaden och skalningen eftersom vårt slutmål är att ta reda på optimeringströsklar där optimeraren ändrar sina val från en strategi till en annan.
I/O-kostnadsuppskattningen verkar vara fast:0,0112613. Jag får samma I/O-kostnad oavsett faktorer som antal rader, antal sorteringskolumner, datatyp och så vidare. Detta är förmodligen för att förklara en del förväntat I/O-arbete.
När det gäller CPU-kostnaden, tyvärr, avslöjar Microsoft inte offentligt de exakta algoritmerna som de använder för sortering. Men bland de vanliga algoritmerna som används för sortering av databasmotorer i allmänhet finns olika implementeringar av merge sort och quicksort. Tack vare ansträngningar som gjorts av Paul White, som är förtjust i att titta på Windows-felsökningsstackspår (inte alla av oss har magen för detta), har vi lite mer insikt i ämnet, publicerat i hans serie "Internals of the Seven SQL Server Sorterar.” Enligt Pauls upptäckter använder den allmänna sorteringsklassen (används i planen ovan) sammanslagningssortering (först intern, sedan övergång till extern). I genomsnitt kräver denna algoritm n log n jämförelser för att sortera n objekt. Med detta i åtanke är det förmodligen ett säkert kort som utgångspunkt att anta att CPU-delen av operatörens kostnad är baserad på en formel som:
Operatörens CPU-kostnad =Naturligtvis kan detta vara en alltför förenkling av den faktiska kostnadsformel som Microsoft använder, men i avsaknad av dokumentation i frågan är detta en första bästa gissning.
Därefter kan du erhålla sorterings-CPU-kostnaderna från två frågeplaner som tagits fram för sortering av olika antal rader, säg 1000 och 2000, och baserat på dessa och ovanstående formel, omvänd konstruktion av jämförelsekostnaden och startkostnaden. För detta ändamål behöver du inte använda en grupperad fråga; det räcker med att bara göra en grundläggande BESTÄLLNING AV. Jag kommer att använda följande två frågor (vi kallar dem Fråga 2 och Fråga 3):
SELECT orderid % 1000000000 as myorderid FROM (SELECT TOP (1000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid; VÄLJ orderid % 1000000000 som myorderid FROM (SELECT TOP (2000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid;
Poängen med att sortera efter resultatet av en beräkning är att tvinga en sorteringsoperator att användas i planen.
Figur 2 visar de relevanta delarna av de två planerna:
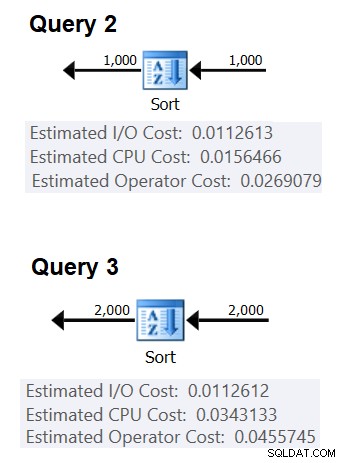
Figur 2:Planer för fråga 2 och fråga 3
För att försöka härleda kostnaden för en jämförelse använder du följande formel:
jämförelsekostnad =
((
/ (
(0,0343133 – 0,0156466) / (2000*LOG(2000) – 1000*LOG(1000)) =2,25061348918698E-06
När det gäller startkostnaden kan du härleda den baserat på båda planerna, t.ex. baserat på planen som sorterar 2000 rader:
startkostnad =0,0343133 – 2000*LOG(2000) * 2,25061348918698E-06 =9,99127891201865>E-01865>E-01865
Och därmed blir vår kostnadsformel för Sortera CPU:
Sorteringsoperatörens CPU-kostnad =9,99127891201865E-05 + @numrows * LOG(@numrows) * 2,25061348918698E-06Genom att använda liknande tekniker kommer du att upptäcka att faktorer som den genomsnittliga radstorleken, antalet beställningskolumner och deras datatyper inte påverkar den beräknade kostnaden för sorterings-CPU. Den enda faktorn som verkar vara relevant är det uppskattade antalet rader. Observera att sorteringen kommer att behöva ett minnesbidrag, och beviljandet är proportionellt mot antalet rader (inte grupper) och den genomsnittliga radstorleken. Men vårt fokus för närvarande är den beräknade operatörskostnaden, och det verkar som om denna uppskattning endast påverkas av det uppskattade antalet rader.
Denna formel verkar förutsäga CPU-kostnaden väl upp till en tröskel på cirka 5 000 rader. Prova med följande siffror:100, 200, 300, 400, 500, 1000, 2000, 3000, 4000, 5000:
SELECT numrows, 9,99127891201865E-05 + numrows * LOG(numrows) * 2,25061348918698E-06 AS predicated cost FROM (VALUES(100), (200), (300), (400)), (10050)), (10050)), , (2000), (3000), (4000), (5000)) AS D(numrows);
Jämför vad formeln förutsäger och de beräknade CPU-kostnaderna som planerna visar för följande frågor:
VÄLJ orderid % 1000000000 som myorderid FROM (SELECT TOP (100) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid; VÄLJ orderid % 1000000000 som myorderid FROM (VÄLJ TOP (200) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid; VÄLJ orderid % 1000000000 som myorderid FROM (SELECT TOP (300) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid; VÄLJ orderid % 1000000000 som myorderid FROM (VÄLJ TOP (400) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid; VÄLJ orderid % 1000000000 som myorderid FROM (SELECT TOP (500) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid; VÄLJ orderid % 1000000000 som myorderid FROM (SELECT TOP (1000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid; VÄLJ orderid % 1000000000 som myorderid FROM (SELECT TOP (2000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid; VÄLJ orderid % 1000000000 som myorderid FROM (SELECT TOP (3000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid; VÄLJ orderid % 1000000000 som myorderid FROM (SELECT TOP (4000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid; VÄLJ orderid % 1000000000 som myorderid FROM (SELECT TOP (5000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid;
Jag fick följande resultat:
numrows predicatedcost estimatedcost ratio ------------------ -------------- -------------- --- ---- 100 0.0011363 0.0011365 1.00018 200 0.0024848 0.0024849 1.00004 300 0.0039510 0.0039511 1.00003 400 0.0054937 0.0054938 1.00002 500 0.0070933 0.0070933 1.00000 1000 0.0156466 0.0156466 1.00000 2000 0.0343133 0.0343133 1.00000 3000 0.0541576 0.0541576 1.00000 4000 0.0747667 0.0747665 1.00000 5000 0.0959445 0.0959442 1.00000
Kolumnen förutspådd kostnad visar förutsägelsen baserat på vår omvända formel, kolumnen beräknad kostnad visar den uppskattade kostnaden som visas i planen och kolumnförhållandet visar förhållandet mellan den senare och den förra.
Predikationen verkar ganska exakt upp till 5 000 rader. Men med siffror större än 5 000 slutar vår omvända formel att fungera bra. Följande fråga ger dig prognoserna för 6K, 7K, 10K, 20K, 100K och 200K rader:
SELECT numrows, 9,99127891201865E-05 + numrows * LOG(numrows) * 2,25061348918698E-06 AS predicated cost FROM (VALUES(6000), (7000), (1000000), (02) (010000), (02) ) AS D(tal);
Använd följande frågor för att få de beräknade CPU-kostnaderna från planerna (notera tipset om att tvinga fram en serieplan eftersom det med större antal rader är mer sannolikt att du får en parallell plan där kostnadsformlerna justeras för parallellitet):
VÄLJ orderid % 1000000000 som myorderid FROM (VÄLJ TOP (6000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid OPTION(MAXDOP 1); VÄLJ orderid % 1000000000 som myorderid FROM (VÄLJ TOP (7000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid OPTION(MAXDOP 1); VÄLJ orderid % 1000000000 som myorderid FROM (VÄLJ TOP (10000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid OPTION(MAXDOP 1); VÄLJ orderid % 1000000000 som myorderid FRÅN (VÄLJ TOP (20000) * FRÅN dbo.Order) SOM BESTÄLLS AV myorderid OPTION(MAXDOP 1); VÄLJ orderid % 1000000000 som myorderid FROM (VÄLJ TOP (100000) * FROM dbo.Orders) SOM BESTÄLLS BY myorderid OPTION(MAXDOP 1); VÄLJ orderid % 1000000000 som myorderid FROM (VÄLJ TOP (200000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid OPTION(MAXDOP 1);
Jag fick följande resultat:
numrows predicatedcost estimatedcost ratio ------------------ -------------- -------------- --- --- 6000 0.117575 0.160970 1.3691 7000 0.139583 0.244848 1.7541 10000 0.207389 0.603420 2.9096 20000 0.445878 1.311710 2.9419 100000 2.591210 7.623920 2.9422 200000 5.494330 16.165700 2.9423
Som du kan se, efter 5 000 rader blir vår formel mindre och mindre exakt, men konstigt nog stabiliseras noggrannhetsförhållandet på cirka 2,94 vid cirka 20 000 rader. Detta innebär att med stora siffror gäller vår formel fortfarande, bara med en högre jämförelsekostnad, och att ungefär mellan 5 000 och 20 000 rader övergår den gradvis från den lägre jämförelsekostnaden till den högre. Men vad kan förklara skillnaden mellan den lilla skalan och den stora skalan? Den goda nyheten är att svaret inte är lika komplicerat som att förena kvantmekanik och allmän relativitet med strängteori. Det är bara det att Microsoft i mindre skala ville ta hänsyn till det faktum att CPU-cachen sannolikt kommer att användas, och för kostnadsskäl antar de en fast cachestorlek.
Så för att räkna ut jämförelsekostnaden i stor skala, vill du använda sorteringen av CPU-kostnader från två planer för siffror över 20 000. Jag kommer att använda 100 000 och 200 000 rader (de två sista raderna i tabellen ovan). Här är formeln för att härleda jämförelsekostnaden:
jämförelsekostnad =(16,1657 – 7,62392) / (200000*LOG(200000) – 100000*LOG(100000)) =6,62193536908588E-06
Nästa, här är formeln för att härleda startkostnaden baserat på planen för 200 000 rader:
startkostnad =16,1657 – 200000*LOG(200000) * 6,62193536908588E-06 =1,35166186417734E-04
Det kan mycket väl vara så att startkostnaden för små och stora skalor är densamma, och att skillnaden vi fick beror på avrundningsfel. I vilket fall som helst, med ett stort antal rader, blir startkostnaden försumbar jämfört med jämförelsens kostnad.
Sammanfattningsvis, här är formeln för sorteringsoperatörens CPU-kostnad för stora tal (>=20000):
Operatörens CPU-kostnad =1,35166186417734E-04 + @numrows * LOG(@numrows) * 6,62193536908588E-06Låt oss testa formelns noggrannhet med 500K, 1M och 10M rader. Följande kod ger dig vår formels förutsägelser:
VÄLJ numrows, 1,35166186417734E-04 + numrows * LOG(numrows) * 6,62193536908588E-06 AS predicated cost FROM (VALUES(500000), (10000000), (1000000), (1000000), (1000000), (1000s)spre;Använd följande frågor för att få de uppskattade CPU-kostnaderna:
VÄLJ orderid % 1000000000 som myorderid FROM (VÄLJ TOP (500000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid OPTION(MAXDOP 1); VÄLJ orderid % 1000000000 som myorderid FROM (VÄLJ TOP (1000000) * FROM dbo.Orders) SOM BESTÄLLS AV myorderid OPTION(MAXDOP 1); SELECT CHECKSUM(NEWID()) som myorderid FROM (SELECT TOP (10000000) O1.orderid FROM dbo.Orders AS O1 CROSS JOIN dbo.Orders AS O2) AS D ORDER BY myorderid OPTION(MAXDOP 1);Jag fick följande resultat:
numrows predicatedcost estimatedcost ratio ------------------ -------------- -------------- --- --- 500000 43,4479 43,448 1,0000 1000000 91,4856 91,486 1,0000 10000000 1067,3300 1067,340 1,0000Det verkar som att vår formel för stora siffror fungerar ganska bra.
Sammanfogar allt
Den totala kostnaden för att tillämpa ett flödesaggregat med explicit sortering för ett litet antal rader (<=5 000 rader) är:
+ + =
0,0112613
+ 9,99127891201865E-05 + @numrows * LOG(@ numrows) * 2,25061348918698E-06
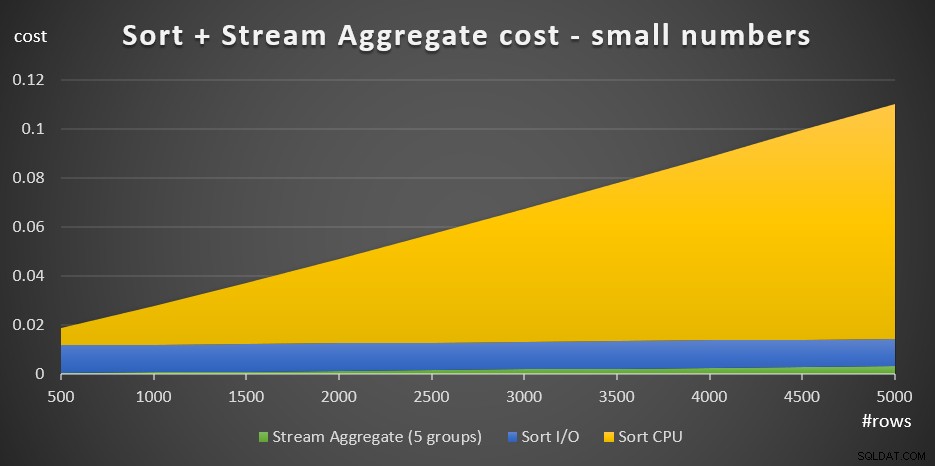
+ @numrows * 0,0000006 + @numrows * 0,0000005Figur 3 har ett områdesdiagram som visar hur denna kostnad skalas.
Figur 3:Sorteringskostnad + Streamaggregat för små antal raderSorterings-CPU-kostnaden är den mest betydande delen av den totala aggregatkostnaden för Sort + Stream. Ändå, med ett litet antal rader, är Stream Aggregate-kostnaden och Sort I/O-delen av kostnaden inte helt försumbara. I visuella termer kan du tydligt se alla tre delarna i diagrammet.
När det gäller ett stort antal rader (>=20 000) är kostnadsformeln:
0,0112613
+ 1,35166186417734E-04 + @numrows * LOG(@numrows) * 6,62193536908588E-06
+ @numrows * 0,000super 0,000sJag såg inte mycket värde i att följa det exakta sättet som jämförelsekostnaden övergår från den lilla till den stora skalan.
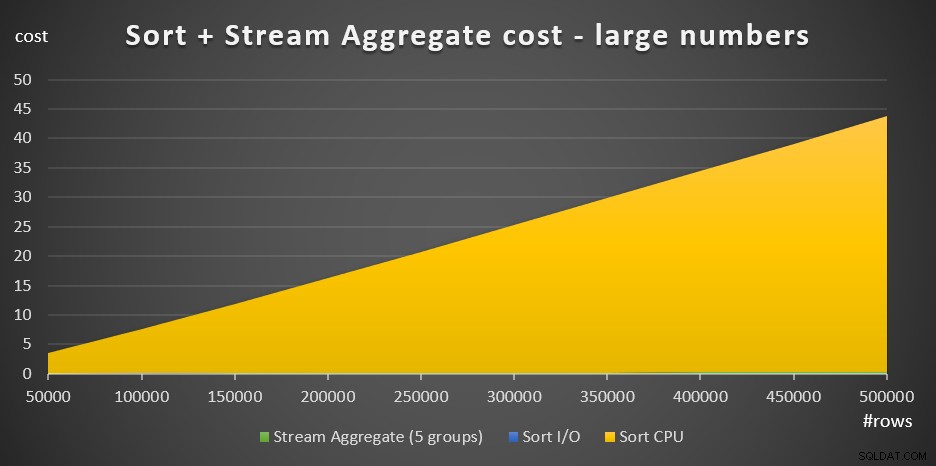
Figur 4 har ett ytdiagram som visar hur kostnaden skalar för stora antal.
Figur 4:Sorteringskostnad + Streamaggregat för ett stort antal raderMed ett stort antal rader är Stream Aggregate-kostnaden och Sort I/O-kostnaden så försumbar jämfört med Sort CPU-kostnaden att de inte ens är synliga för blotta ögat i diagrammet. Dessutom är den del av Sort CPU-kostnaden som tillskrivs startarbetet också försumbar. Därför är den enda delen av kostnadskalkylen som verkligen är meningsfull den totala jämförelsekostnaden:
@numrows * LOG(@numrows) *Detta innebär att när du behöver utvärdera skalningen av Sort + Stream Aggregate-strategin kan du förenkla den till enbart den här dominerande delen. Om du till exempel behöver utvärdera hur kostnaden skulle skala från 100 000 rader till 100 000 000 rader, kan du använda formeln (notera att jämförelsekostnaden är irrelevant):
(100000000 * LOG(100000000)*) / (100000 * LOG(100000)*) =1600Detta talar om att när antalet rader ökar från 100 000 med en faktor 1 000 till 100 000 000, så ökar den beräknade kostnaden med en faktor på 1 600.
Skalning från 1 000 000 till 1 000 000 000 rader beräknas som:
(1000000000 * LOG(1000000000)) / (1000000 * LOG(1000000)) =1500Det vill säga när antalet rader ökar från 1 000 000 med en faktor 1 000, ökar den beräknade kostnaden med en faktor 1 500.
Det här är intressanta observationer om hur strategin Sort + Stream Aggregate skalas. På grund av dess mycket låga startkostnad och extra linjära skalning, skulle du förvänta dig att den här strategin skulle klara sig bra med mycket litet antal rader, men inte så bra med stora antal. Det faktum att Stream Aggregate-operatören ensam står för en så liten bråkdel av kostnaden jämfört med när en sortering också behövs, säger dig att du kan få betydligt bättre prestanda om situationen är sådan att du kan skapa ett stödjande index .
I nästa del av serien kommer jag att täcka skalningen av Hash Aggregate-algoritmen. Om du gillar den här övningen att försöka räkna ut kostnadsformler, se om du kan räkna ut det för den här algoritmen. Det som är viktigt är att ta reda på vilka faktorer som påverkar det, hur det skalas och villkoren där det fungerar bättre än de andra algoritmerna.