Detta är den tredje delen i en serie om lösningar på nummerseriegeneratorutmaningen. I del 1 behandlade jag lösningar som genererar raderna i farten. I del 2 behandlade jag lösningar som frågar efter en fysisk bastabell som du förfyller med rader. Den här månaden kommer jag att fokusera på en fascinerande teknik som kan användas för att hantera vår utmaning, men som också har intressanta tillämpningar långt bortom den. Jag känner inte till ett officiellt namn för tekniken, men den liknar i konceptet en horisontell partitionseliminering, så jag kommer att hänvisa till den informellt som horisontal unit elimination Metod. Tekniken kan ha intressanta positiva prestationsfördelar, men det finns också varningar som du måste vara medveten om, där den under vissa förhållanden kan medföra prestationsstraff.
Tack igen till Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea och Paul White för att du delar med dig av dina idéer och kommentarer.
Jag ska göra mina tester i tempdb och aktivera tidsstatistik:
SET NOCOUNT ON; USE tempdb; SET STATISTICS TIME ON;
Tidigare idéer
Tekniken för eliminering av horisontella enheter kan användas som ett alternativ till logiken för eliminering av kolumner, eller eliminering av vertikala enheter teknik, som jag förlitade mig på i flera av lösningarna som jag behandlade tidigare. Du kan läsa om grunderna för kolumnelimineringslogik med tabelluttryck i Fundamentals of table expressions, Del 3 – Härledda tabeller, optimeringsöverväganden under "Kolumnprojektion och ett ord om SELECT *."
Grundidén med tekniken för eliminering av vertikala enheter är att om du har ett kapslat tabelluttryck som returnerar kolumnerna x och y, och din yttre fråga endast refererar till kolumn x, eliminerar frågekompileringsprocessen y från det initiala frågeträdet, och därför planen behöver inte utvärdera det. Detta har flera positiva optimeringsrelaterade implikationer, som att uppnå indextäckning enbart med x, och om y är ett resultat av en beräkning behöver du inte utvärdera y:s underliggande uttryck alls. Denna idé var kärnan i Alan Bursteins lösning. Jag förlitade mig också på det i flera av de andra lösningarna som jag täckte, till exempel med funktionen dbo.GetNumsAlanCharlieItzikBatch (från del 1), funktionerna dbo.GetNumsJohn2DaveObbishAlanCharlieItzik och dbo.GetNumsJohn2DaveObbishAlanCharrom, och andra Parts. Som ett exempel kommer jag att använda dbo.GetNumsAlanCharlieItzikBatch som baslinjelösning med den vertikala elimineringslogiken.
Som en påminnelse använder den här lösningen en sammanfogning med en dummy-tabell som har ett kolumnlagerindex för att få batchbearbetning. Här är koden för att skapa dummy-tabellen:
DROP TABLE IF EXISTS dbo.BatchMe; GO CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
Och här är koden med definitionen av dbo.GetNumsAlanCharlieItzikBatch-funktionen:
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1)
rownum AS rn,
@high + 1 - rownum AS op,
@low - 1 + rownum AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum;
GO Jag använde följande kod för att testa funktionens prestanda med 100 miljoner rader, och returnerade den beräknade resultatkolumnen n (manipulation av resultatet av funktionen ROW_NUMBER), sorterad efter n:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) ORDER BY n OPTION(MAXDOP 1);
Här är tidsstatistiken som jag fick för det här testet:
CPU-tid =9328 ms, förfluten tid =9330 ms.Jag använde följande kod för att testa funktionens prestanda med 100 miljoner rader, och returnerade kolumnen rn (direkt, omanipulerad, resultat av funktionen ROW_NUMBER), sorterad efter rn:
DECLARE @n AS BIGINT; SELECT @n = rn FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) ORDER BY rn OPTION(MAXDOP 1);
Här är tidsstatistiken som jag fick för det här testet:
CPU-tid =7296 ms, förfluten tid =7291 ms.Låt oss granska de viktiga idéerna som är inbäddade i den här lösningen.
Med hjälp av logik för att eliminera kolumner kom alan på idén att inte bara returnera en kolumn med nummerserien, utan tre:
- Kolumn rn representerar ett omanipulerat resultat av funktionen ROW_NUMBER, som börjar med 1. Det är billigt att beräkna. Det är ordningsbevarande både när du tillhandahåller konstanter och när du tillhandahåller icke-konstanter (variabler, kolumner) som indata till funktionen. Det betyder att när din yttre fråga använder ORDER BY rn, får du ingen sorteringsoperator i planen.
- Kolumn n representerar en beräkning baserad på @low, en konstant och rownum (resultat av funktionen ROW_NUMBER). Det är ordningsbevarande med avseende på rownum när du tillhandahåller konstanter som indata till funktionen. Det är tack vare Charlies insikt om konstant vikning (se del 1 för detaljer). Det är dock inte ordningsbevarande när du tillhandahåller icke-konstanter som indata, eftersom du inte får konstant vikning. Jag ska visa detta senare i avsnittet om varningar.
- Kolumn op representerar n i motsatt ordning. Det är ett resultat av en beräkning och det är inte ordningsbevarande.
Om du förlitar dig på kolumnelimineringslogiken, om du behöver returnera en nummerserie som börjar med 1, frågar du kolumn rn, vilket är billigare än att fråga n. Om du behöver en nummerserie som börjar med ett annat värde än 1, frågar du n och betalar extrakostnaden. Om du behöver resultatet sorterat efter nummerkolumnen, med konstanter som indata, kan du använda antingen ORDER BY rn eller ORDER BY n. Men med icke-konstanter som ingångar vill du se till att använda ORDER BY rn. Det kan vara en bra idé att alltid hålla sig till att använda ORDER BY rn när du behöver resultatet beställt för att vara på den säkra sidan.
Idén för att eliminera horisontella enheter liknar idén för att eliminera vertikala enheter, bara den gäller uppsättningar av rader istället för uppsättningar av kolumner. Faktum är att Joe Obbish förlitade sig på denna idé i sin funktion dbo.GetNumsObbish (från del 2), och vi kommer att ta det ett steg längre. I sin lösning förenade Joe flera frågor som representerar osammanhängande delintervall av tal, med hjälp av ett filter i WHERE-satsen för varje fråga för att definiera tillämpligheten av underintervallet. När du anropar funktionen och skickar konstanta inmatningar som representerar avgränsare för ditt önskade intervall, eliminerar SQL Server de otillämpliga frågorna vid kompilering, så att planen inte ens speglar dem.
Eliminering av horisontell enhet, kompileringstid kontra körtid
Det kanske vore en bra idé att börja med att demonstrera begreppet horisontell enhetseliminering i ett mer generellt fall, och även diskutera en viktig distinktion mellan kompileringstid och körtidseliminering. Sedan kan vi diskutera hur vi ska tillämpa idén på vår nummerserieutmaning.
Jag använder tre tabeller som heter dbo.T1, dbo.T2 och dbo.T3 i mitt exempel. Använd följande DDL- och DML-kod för att skapa och fylla i dessa tabeller:
DROP TABLE IF EXISTS dbo.T1, dbo.T2, dbo.T3; GO CREATE TABLE dbo.T1(col1 INT); INSERT INTO dbo.T1(col1) VALUES(1); CREATE TABLE dbo.T2(col1 INT); INSERT INTO dbo.T2(col1) VALUES(2); CREATE TABLE dbo.T3(col1 INT); INSERT INTO dbo.T3(col1) VALUES(3);
Anta att du vill implementera en inline TVF som heter dbo.OneTable som accepterar ett av ovanstående tre tabellnamn som indata och returnerar data från den begärda tabellen. Baserat på konceptet för att eliminera horisontella enheter kan du implementera funktionen så här:
CREATE OR ALTER FUNCTION dbo.OneTable(@WhichTable AS NVARCHAR(257)) RETURNS TABLE AS RETURN SELECT col1 FROM dbo.T1 WHERE @WhichTable = N'dbo.T1' UNION ALL SELECT col1 FROM dbo.T2 WHERE @WhichTable = N'dbo.T2' UNION ALL SELECT col1 FROM dbo.T3 WHERE @WhichTable = N'dbo.T3'; GO
Kom ihåg att en inline TVF tillämpar parameterinbäddning. Detta innebär att när du skickar en konstant som N'dbo.T2' som indata, ersätter inliningsprocessen alla referenser till @WhichTable med konstanten före optimering . Elimineringsprocessen kan sedan ta bort referenserna till T1 och T3 från det initiala frågeträdet, och på så sätt resulterar frågeoptimering i en plan som endast refererar till T2. Låt oss testa den här idén med följande fråga:
SELECT * FROM dbo.OneTable(N'dbo.T2');
Planen för denna fråga visas i figur 1.
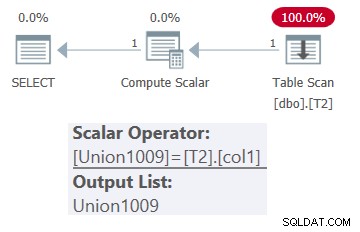 Figur 1:Planera för dbo.OneTable med konstant input
Figur 1:Planera för dbo.OneTable med konstant input
Som du kan se visas endast tabell T2 i planen.
Saker och ting är lite knepigare när du skickar en icke-konstant som input. Detta kan vara fallet när du använder en variabel, en procedurparameter eller skickar en kolumn via APPLY. Ingångsvärdet är antingen okänt vid kompileringstidpunkten, eller också måste parametrerad planåteranvändningspotential beaktas.
Optimeraren kan inte eliminera någon av tabellerna från planen, men den har fortfarande ett knep. Den kan använda startfilteroperatorer ovanför underträden som kommer åt tabellerna och köra endast det relevanta underträdet baserat på körtidsvärdet för @WhichTable. Använd följande kod för att testa denna strategi:
DECLARE @T AS NVARCHAR(257) = N'dbo.T2'; SELECT * FROM dbo.OneTable(@T);
Planen för detta utförande visas i figur 2:
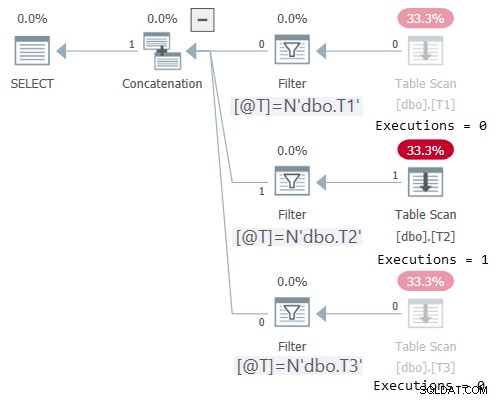 Figur 2:Plan för dbo.OneTable med icke-konstant indata
Figur 2:Plan för dbo.OneTable med icke-konstant indata
Plan Explorer gör det underbart uppenbart att se att endast det tillämpliga underträdet exekverades (Executions =1), och grånar ut underträden som inte exekveras (Executions =0). Dessutom visar STATISTICS IO I/O-information endast för tabellen som var åtkomst:
Tabell 'T2'. Scan count 1, logisk läser 1, fysisk läser 0, sidserver läser 0, läser framåt läser 0, sidserver läser framåt läser 0, lob logisk läser 0, lob fysisk läser 0, lob sidserver läser 0, lob läs- ahead läser 0, lob page server read-ahead läser 0.Tillämpa logik för att eliminera horisontella enheter på nummerserieutmaningen
Som nämnts kan du tillämpa konceptet för att eliminera horisontella enheter genom att modifiera någon av de tidigare lösningarna som för närvarande använder vertikal elimineringslogik. Jag använder funktionen dbo.GetNumsAlanCharlieItzikBatch som utgångspunkt för mitt exempel.
Kom ihåg att Joe Obbish använde horisontell enhetseliminering för att extrahera de relevanta disjunkta underområdena i nummerserien. Vi kommer att använda konceptet för att horisontellt separera den billigare beräkningen (rn) där @låg =1 från den dyrare beräkningen (n) där @låg <> 1.
Medan vi håller på kan vi experimentera genom att lägga till Jeff Modens idé i sin fnTally-funktion, där han använder en vaktpostrad med värdet 0 för fall där intervallet börjar med @low =0.
Så vi har fyra horisontella enheter:
- Sentinel-rad med 0 där @low =0, med n =0
- TOP (@high) rader där @low =0, med billig n =rownum, och op =@high – rownum
- TOP (@high) rader där @low =1, med billig n =rownum, och op =@high + 1 – rownum
- TOP(@hög – @låg + 1) rader där @låg <> 0 OCH @låg <> 1, med dyrare n =@låg – 1 + radnummer, och op =@hög + 1 – radnummer
Den här lösningen kombinerar idéer från Alan, Charlie, Joe, Jeff och mig själv, så vi kallar batchlägesversionen av funktionen dbo.GetNumsAlanCharlieJoeJeffItzikBatch.
Kom först ihåg att se till att du fortfarande har dummytabellen dbo.BatchMe närvarande för att få batchbearbetning i vår lösning, eller använd följande kod om du inte har det:
DROP TABLE IF EXISTS dbo.BatchMe; GO CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
Här är koden med definitionen av dbo.GetNumsAlanCharlieJoeJeffItzikBatch-funktionen:
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieJoeJeffItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT @low AS n, @high AS op WHERE @low = 0 AND @high > @low
UNION ALL
SELECT TOP(@high)
rownum AS n,
@high - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
WHERE @low = 0
ORDER BY rownum
UNION ALL
SELECT TOP(@high)
rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
WHERE @low = 1
ORDER BY rownum
UNION ALL
SELECT TOP(@high - @low + 1)
@low - 1 + rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
WHERE @low <> 0 AND @low <> 1
ORDER BY rownum;
GO Viktigt:Konceptet för att eliminera horisontella enheter är utan tvekan mer komplicerat att implementera än det vertikala, så varför bry sig? Eftersom det tar bort ansvaret att välja rätt kolumn från användaren. Användaren behöver bara oroa sig för att fråga efter en kolumn som heter n, i motsats till att komma ihåg att använda rn när intervallet börjar med 1, och n annars.
Låt oss börja med att testa lösningen med konstanta ingångar 1 och 100 000 000 och be om att resultatet ska beställas:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeJeffItzikBatch(1, 100000000) ORDER BY n OPTION(MAXDOP 1);
Planen för detta utförande visas i figur 3.
 Figur 3:Plan för dbo.GetNumsAlanCharlieJoeJeffItzikBatch,(M)
Figur 3:Plan för dbo.GetNumsAlanCharlieJoeJeffItzikBatch,(M)
Observera att den enda returnerade kolumnen är baserad på det direkta, omanipulerade uttrycket ROW_NUMBER (Expr1313). Observera också att det inte finns något behov av att sortera i planen.
Jag fick följande tidsstatistik för denna körning:
CPU-tid =7359 ms, förfluten tid =7354 ms.Körtiden återspeglar på ett adekvat sätt det faktum att planen använder batchläge, det omanipulerade uttrycket ROW_NUMBER och ingen sortering.
Testa sedan funktionen med det konstanta området 0 till 99 999 999:
DECLARE @n AS BIGINT; SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeJeffItzikBatch(0, 99999999) ORDER BY n OPTION(MAXDOP 1);
Planen för detta utförande visas i figur 4.
Planen använder en Merge Join (Concatenation)-operator för att slå samman sentinel-raden med värdet 0 och resten. Även om den andra delen är lika effektiv som tidigare, tar sammanslagningslogiken en ganska stor avgift på cirka 26 % på körtiden, vilket resulterar i följande tidsstatistik:
Låt oss testa funktionen med konstantområdet 2 till 100 000 001:
Planen för detta utförande visas i figur 5.
Den här gången finns det ingen dyr sammanslagningslogik eftersom vaktpostdelen är irrelevant. Observera dock att den returnerade kolumnen är det manipulerade uttrycket @low – 1 + rownum, som efter parameterinbäddning/inlining och konstant vikning blev 1 + rownum.
Här är tidsstatistiken som jag fick för den här exekveringen:
Som förväntat är detta inte lika snabbt som med ett intervall som börjar med 1, men intressant nog snabbare än med ett intervall som börjar med 0.
Med tanke på att tekniken med sentinel-raden med värdet 0 verkar vara långsammare än att tillämpa manipulation på rownum, är det vettigt att helt enkelt undvika det. Detta för oss till en förenklad horisontell elimineringsbaserad lösning som blandar idéerna från Alan, Charlie, Joe och mig själv. Jag kallar funktionen med denna lösning dbo.GetNumsAlanCharlieJoeItzikBatch. Här är funktionens definition:
Låt oss testa det med intervallet 1 till 100M:
Planen är densamma som den som visas tidigare i figur 3, som förväntat.
Följaktligen fick jag följande tidsstatistik:
Testa det med intervallet 0 till 99 999 999:
Den här gången får du samma plan som den som visades tidigare i figur 5—inte figur 4.
Här är tidsstatistiken som jag fick för den här körningen:
Testa det med intervallet 2 till 100 000 001:
Återigen får du samma plan som den som visades tidigare i figur 5.
Jag fick följande tidsstatistik för denna körning:
Med teknikerna för eliminering av både vertikala och horisontella enheter fungerar saker idealiskt så länge du skickar konstanter som indata. Du måste dock vara medveten om varningar som kan resultera i prestationsstraff när du passerar icke-konstanta ingångar. Tekniken för att eliminera vertikala enheter har färre problem, och de problem som finns är lättare att hantera, så låt oss börja med det.
Kom ihåg att vi i den här artikeln använde funktionen dbo.GetNumsAlanCharlieItzikBatch som vårt exempel som bygger på konceptet för att eliminera vertikala enheter. Låt oss köra en serie tester med icke-konstanta indata, till exempel variabler.
Som vårt första test kommer vi att returnera rn och fråga efter data som beställts av rn:
Kom ihåg att rn representerar det omanipulerade uttrycket ROW_NUMBER, så det faktum att vi använder icke-konstanta indata har ingen speciell betydelse i det här fallet. Det finns inget behov av explicit sortering i planen.
Jag fick följande tidsstatistik för denna körning:
Dessa siffror representerar det ideala fallet.
I nästa test, ordna resultatraderna efter n:
Planen för detta utförande visas i figur 6.
Ser du problemet? Efter inlining ersattes @low med @mylow—inte med värdet i @mylow, vilket är 1. Följaktligen skedde inte konstant vikning, och därför är n inte ordningsbevarande med avseende på rownum. Detta resulterade i en explicit sortering i planen.
Här är tidsstatistiken som jag fick för den här exekveringen:
Exekveringstiden nästan tredubblades jämfört med när explicit sortering inte behövdes.
En enkel lösning är att använda Alan Bursteins ursprungliga idé att alltid beställa efter rn när du behöver resultatet beställt, både när du returnerar rn och när du returnerar n, som så:
Den här gången finns det ingen explicit sortering i planen.
Jag fick följande tidsstatistik för denna körning:
Siffrorna återspeglar på ett adekvat sätt det faktum att du returnerar det manipulerade uttrycket, men inte medför någon explicit sortering.
Med lösningar som är baserade på tekniken för eliminering av horisontella enheter, såsom vår dbo.GetNumsAlanCharlieJoeItzikBatch-funktion, är situationen mer komplicerad när man använder icke-konstanta indata.
Låt oss först testa funktionen med ett mycket litet intervall på 10 siffror:
Planen för detta utförande visas i figur 7.
Det finns en mycket alarmerande sida av denna plan. Observera att filteroperatorerna visas nedan de bästa operatörerna! I varje givet anrop till funktionen med icke-konstanta ingångar kommer naturligtvis alltid en av grenarna under operatören Konkatenering alltid att ha ett falskt filtertillstånd. Båda toppoperatörerna ber dock om ett antal rader som inte är noll. Så topoperatorn ovanför operatorn med det falska filtervillkoret kommer att fråga efter rader och kommer aldrig att bli nöjd eftersom filteroperatorn kommer att fortsätta att kassera alla rader som den kommer att få från sin undernod. Arbetet i underträdet under filteroperatorn måste köras till slut. I vårt fall betyder detta att underträdet kommer att gå igenom arbetet med att generera 4B rader, som filteroperatorn kommer att förkasta. Du undrar varför filteroperatorn stör sig på att begära rader från sin undernod, men det verkar som om det är så det fungerar för närvarande. Det är svårt att se detta med en statisk plan. Det är lättare att se detta live, till exempel med alternativet för körning av frågor i SentryOne Plan Explorer, som visas i figur 8. Prova det.
Det tog det här testet 9:15 minuter att slutföra på min maskin, och kom ihåg att begäran var att returnera ett intervall på 10 nummer.
Låt oss fundera på om det finns ett sätt att undvika att aktivera det irrelevanta underträdet i sin helhet. För att uppnå detta skulle du vilja att startfilteroperatorerna visas ovanför toppoperatörerna istället för under dem. Om du läser Fundamentals of table expressions, Del 4 – Härledda tabeller, optimeringsöverväganden, fortsättning, vet du att ett TOP-filter förhindrar att tabelluttryck tas bort. Så allt du behöver göra är att placera TOP-frågan i en härledd tabell och tillämpa filtret i en yttre fråga mot den härledda tabellen.
Här är vår modifierade funktion som implementerar detta trick:
Som väntat fortsätter körningar med konstanter att bete sig och prestera på samma sätt som utan tricket.
När det gäller icke-konstanta ingångar, nu med små intervall är det väldigt snabbt. Här är ett test med ett intervall på 10 siffror:
Planen för detta utförande visas i figur 9.
Observera att den önskade effekten av att placera filteroperatorerna ovanför toppoperatorerna uppnåddes. Ordningskolumnen n behandlas dock som ett resultat av manipulation och anses därför inte vara en ordningsbevarande kolumn med avseende på rownum. Följaktligen finns det explicit sortering i planen.
Testa funktionen med ett stort intervall på 100 miljoner nummer:
Jag fick följande tidsstatistik:
Vilken otur; det var nästan perfekt!
Figur 10 har en sammanfattning av tidsstatistiken för de olika lösningarna.
Så vad har vi lärt oss av allt detta? Jag antar att inte göra det igen! Skojar bara. Vi lärde oss att det är säkrare att använda konceptet för vertikal eliminering som i dbo.GetNumsAlanCharlieItzikBatch, som avslöjar både det omanipulerade ROW_NUMBER-resultatet (rn) och det manipulerade (n). Se bara till att när du behöver returnera det beställda resultatet, beställ alltid efter rn, oavsett om du returnerar rn eller n.
Om du är helt säker på att din lösning alltid kommer att användas med konstanter som indata, kan du använda konceptet för att eliminera horisontella enheter. Detta kommer att resultera i en mer intuitiv lösning för användaren, eftersom de kommer att interagera med en kolumn för de stigande värdena. Jag skulle fortfarande föreslå att du använder tricket med de härledda tabellerna för att förhindra att de urlas och placerar filteroperatorerna ovanför toppoperatorerna om funktionen någonsin används med icke-konstanta indata, bara för att vara på den säkra sidan.
Vi är fortfarande inte klara än. Nästa månad fortsätter jag att utforska ytterligare lösningar. Figur 4:Plan för dbo.GetNumsAlanCharlieJoeJeffItzikBatch
Figur 4:Plan för dbo.GetNumsAlanCharlieJoeJeffItzikBatch DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeJeffItzikBatch(2, 100000001) ORDER BY n OPTION(MAXDOP 1);
 Figur 5:Plan för dbo.GetNumsAlanCharlieJoeJeffItzikBatch0,02)02(0,02)
Figur 5:Plan för dbo.GetNumsAlanCharlieJoeJeffItzikBatch0,02)02(0,02) Ta bort 0-vaktraden
CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieJoeItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high)
rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
WHERE @low = 1
ORDER BY rownum
UNION ALL
SELECT TOP(@high - @low + 1)
@low - 1 + rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
WHERE @low <> 1
ORDER BY rownum;
GO DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(1, 100000000) ORDER BY n OPTION(MAXDOP 1);
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(0, 99999999) ORDER BY n OPTION(MAXDOP 1);
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(2, 100000001) ORDER BY n OPTION(MAXDOP 1);
Varningar vid användning av icke-konstanta indata
DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 100000000;
DECLARE @n AS BIGINT;
SELECT @n = rn FROM dbo.GetNumsAlanCharlieItzikBatch(@mylow, @myhigh) ORDER BY rn OPTION(MAXDOP 1);
DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 100000000;
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(@mylow, @myhigh) ORDER BY n OPTION(MAXDOP 1);
 Figur 6:Planera för dbo.GetNumsAlanCharlieItzikBatch(@)mylow, @beställning n
Figur 6:Planera för dbo.GetNumsAlanCharlieItzikBatch(@)mylow, @beställning n DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 100000000;
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(@mylow, @myhigh) ORDER BY rn OPTION(MAXDOP 1);
DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 10;
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(@mylow, @myhigh) ORDER BY n OPTION(MAXDOP 1);
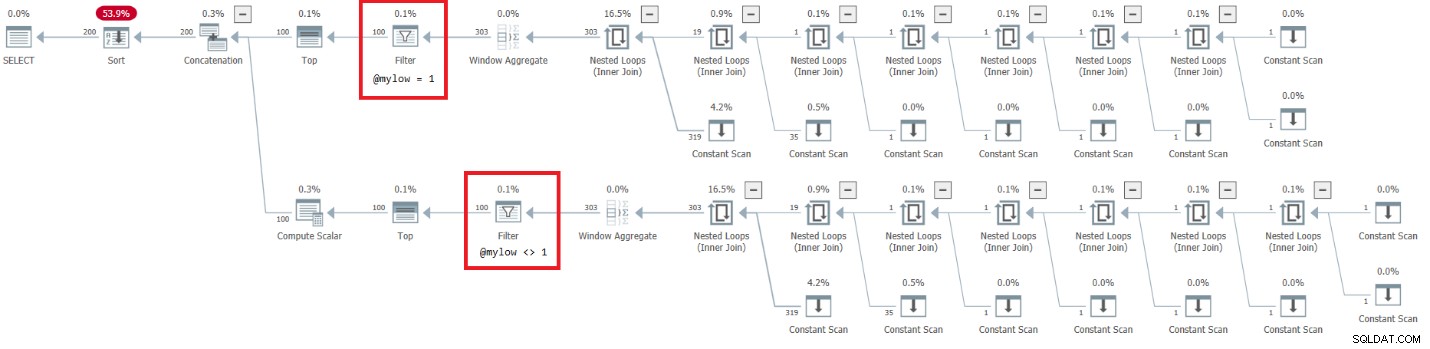 Figur 7:Plan för dbo.GetNumsAlanCharlieJoeItzikBatch(@mylow), @myhigh)
Figur 7:Plan för dbo.GetNumsAlanCharlieJoeItzikBatch(@mylow), @myhigh) 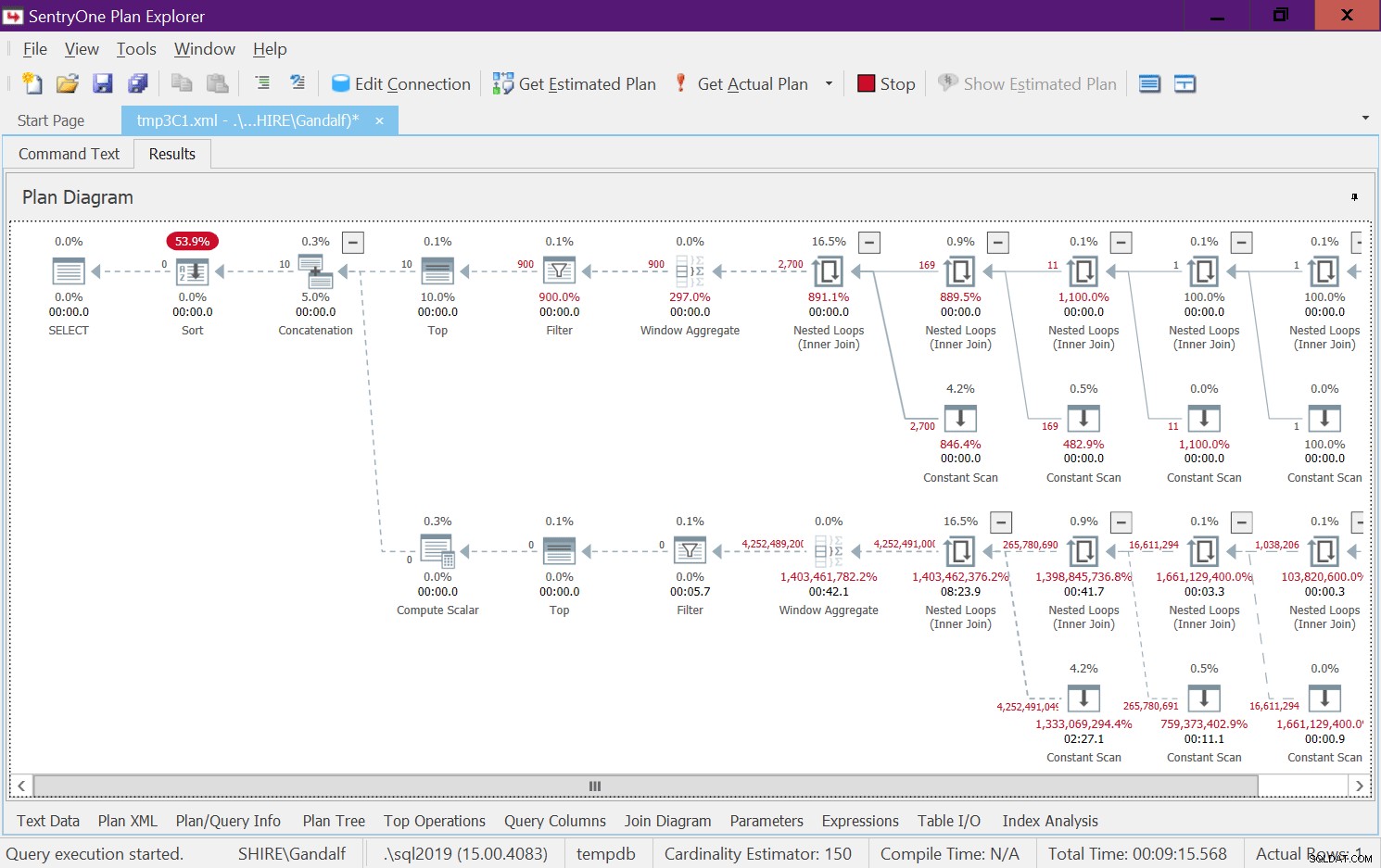 Figur 8:Live frågestatistik för dbo.GetNumsAlanCharlieJoeIghmylow,chmy @hi@highmylowBat,chmy
Figur 8:Live frågestatistik för dbo.GetNumsAlanCharlieJoeIghmylow,chmy @hi@highmylowBat,chmy CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieJoeItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT *
FROM ( SELECT TOP(@high)
rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum ) AS D1
WHERE @low = 1
UNION ALL
SELECT *
FROM ( SELECT TOP(@high - @low + 1)
@low - 1 + rownum AS n,
@high + 1 - rownum AS op
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum ) AS D2
WHERE @low <> 1;
GO DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 10;
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(@mylow, @myhigh) ORDER BY n OPTION(MAXDOP 1);
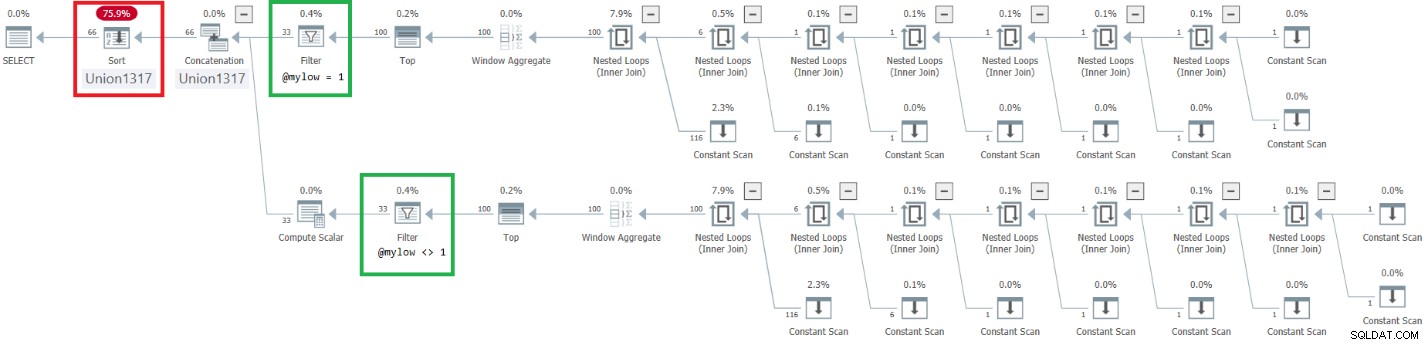 Figur 9:Planera för förbättrad dbo.GetNumsAlanCharlieJoeItzikBatch @my@high)
Figur 9:Planera för förbättrad dbo.GetNumsAlanCharlieJoeItzikBatch @my@high)DECLARE @mylow AS BIGINT = 1, @myhigh AS BIGINT = 100000000;
DECLARE @n AS BIGINT;
SELECT @n = n FROM dbo.GetNumsAlanCharlieJoeItzikBatch(@mylow, @myhigh) ORDER BY n OPTION(MAXDOP 1);
Prestanda sammanfattning och insikter
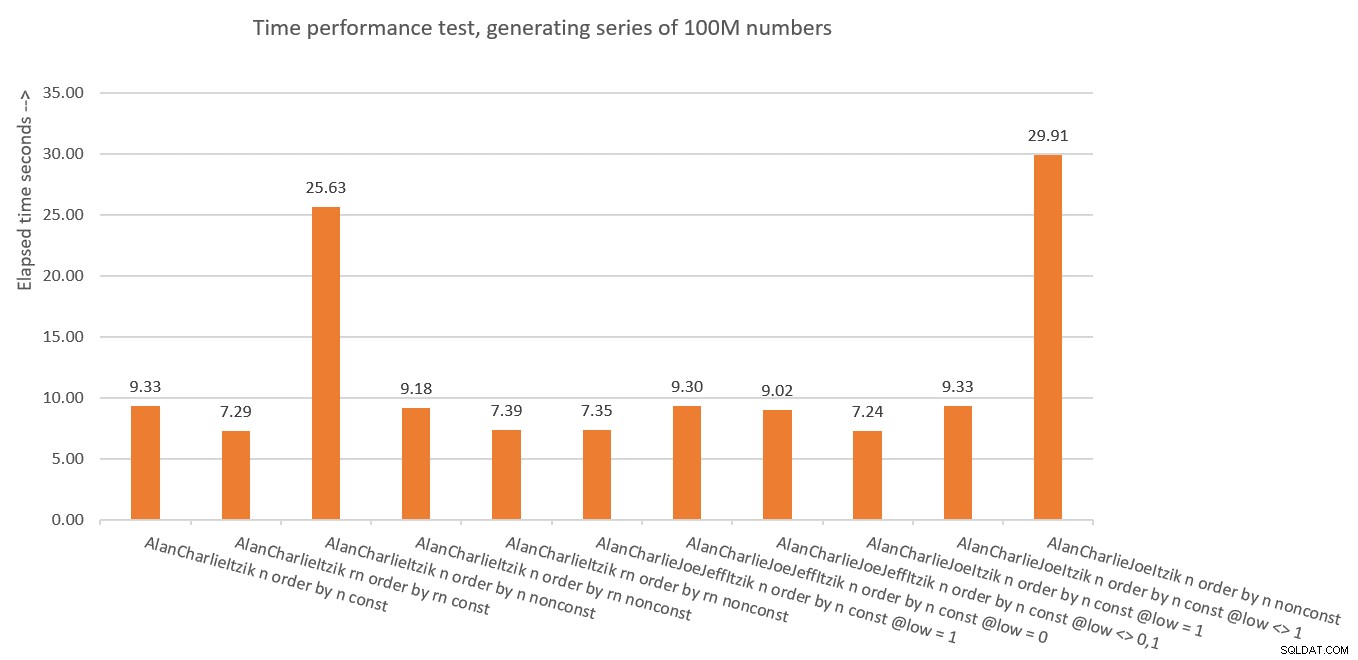 Figur 10:Tidsprestandasammanfattning av lösningar
Figur 10:Tidsprestandasammanfattning av lösningar
