En viktig del av frågejustering är att förstå de algoritmer som är tillgängliga för optimeraren för att hantera olika frågekonstruktioner, t.ex. filtrering, sammanfogning, gruppering och aggregering, och hur de skalas. Denna kunskap hjälper dig att förbereda en optimal fysisk miljö för dina frågor, som att skapa rätt index. Det hjälper dig också intuitivt att känna av vilken algoritm du bör förvänta dig att se i planen under en viss uppsättning omständigheter, baserat på din förtrogenhet med tröskelvärdena där optimeraren ska byta från en algoritm till en annan. När du sedan ställer in frågor som ger dåligt resultat kan du lättare upptäcka områden i frågeplanen där optimeraren kan ha gjort suboptimala val, till exempel på grund av felaktiga uppskattningar av kardinalitet, och vidta åtgärder för att åtgärda dessa.
En annan viktig del av frågejustering är att tänka utanför lådan – bortom de algoritmer som är tillgängliga för optimeraren när de använder de uppenbara verktygen. Vara kreativ. Säg att du har en fråga som presterar dåligt trots att du ordnat den optimala fysiska miljön. För frågekonstruktionerna som du använde är de tillgängliga algoritmerna för optimeraren x, y och z, och optimeraren valde det bästa den kunde under omständigheterna. Ändå fungerar frågan dåligt. Kan du föreställa dig en teoretisk plan med en algoritm som kan ge en mycket bättre resultatfråga? Om du kan föreställa dig det, är chansen stor att du kommer att kunna uppnå det med någon fråga omskrivning, kanske med mindre uppenbara frågekonstruktioner för uppgiften.
I den här artikelserien fokuserar jag på att gruppera och aggregera data. Jag börjar med att gå igenom de algoritmer som är tillgängliga för optimeraren när du använder grupperade frågor. Jag kommer sedan att beskriva scenarier där ingen av de befintliga algoritmerna fungerar bra och visar omskrivningar av frågor som faktiskt resulterar i utmärkt prestanda och skalning.
Jag skulle vilja tacka Craig Freedman, Vassilis Papadimos och Joe Sack, medlemmar i skärningspunkten mellan uppsättningen smartaste människor på planeten och uppsättningen SQL Server-utvecklare, för att de svarade på mina frågor om frågeoptimering!
För exempeldata använder jag en databas som heter PerformanceV3. Du kan ladda ner ett skript för att skapa och fylla i databasen härifrån. Jag använder en tabell som heter dbo.Orders, som är fylld med 1 000 000 rader. Den här tabellen har ett par index som inte behövs och kan störa mina exempel, så kör följande kod för att ta bort de onödiga indexen:
DROP INDEX idx_nc_sid_od_cid ON dbo.Orders; DROP INDEX idx_unc_od_oid_i_cid_eid ON dbo.Orders;
De enda två indexen som finns kvar i den här tabellen är ett klustrat index som kallas idx_cl_od i orderdate-kolumnen och ett icke-klustrat unikt index som heter PK_Orders i orderid-kolumnen, vilket upprätthåller den primära nyckelbegränsningen.
EXEC sys.sp_helpindex 'dbo.Orders';
index_name index_description index_keys ----------- ----------------------------------------------------- ----------- idx_cl_od clustered located on PRIMARY orderdate PK_Orders nonclustered, unique, primary key located on PRIMARY orderid
Befintliga algoritmer
SQL Server stöder två huvudalgoritmer för aggregering av data:Stream Aggregate och Hash Aggregate. Med grupperade frågor kräver Stream Aggregate-algoritmen att data sorteras efter de grupperade kolumnerna, så du måste skilja mellan två fall. Den ena är ett förbeställt strömaggregat, t.ex. när data erhålls förbeställd från ett index. En annan är ett icke-förbeställt Stream Aggregate, där ett extra steg krävs för att explicit sortera indata. Dessa två fall skalas väldigt olika så du kan lika gärna betrakta dem som två olika algoritmer.
Algoritmen för hashaggregat organiserar grupperna och deras aggregat i en hashtabell. Det kräver inte att ingången beställs.
Med tillräckligt med data överväger optimeraren att parallellisera arbetet genom att tillämpa vad som kallas ett lokalt-globalt aggregat. I ett sådant fall delas inmatningen upp i flera trådar, och varje tråd tillämpar en av de tidigare nämnda algoritmerna för att lokalt aggregera sin delmängd av rader. Ett globalt aggregat använder sedan en av de tidigare nämnda algoritmerna för att aggregera resultaten av de lokala aggregaten.
I den här artikeln fokuserar jag på den förbeställda Stream Aggregate-algoritmen och dess skalning. I framtida delar av den här serien kommer jag att täcka andra algoritmer och beskriva tröskelvärdena där optimeraren växlar från en till en annan, och när du bör överväga omskrivningar av frågor.
Förbeställt Stream Aggregate
Givet en grupperad fråga med en icke-tom grupperingsuppsättning (uppsättningen uttryck som du grupperar efter), kräver Stream Aggregate-algoritmen att inmatningsraderna ordnas efter uttrycken som bildar grupperingsuppsättningen. När algoritmen bearbetar den första raden i en grupp, initierar den en medlem som håller det mellanliggande aggregatvärdet med det relevanta värdet (t.ex. första radens värde för ett MAX-aggregat). När den bearbetar en icke-första rad i gruppen tilldelar den den medlemmen resultatet av en beräkning som involverar det mellanliggande sammanlagda värdet och den nya radens värde (t.ex. maxvärdet mellan det mellanliggande sammanlagda värdet och det nya värdet). Så snart någon av grupperingsuppsättningens medlemmar ändrar sitt värde, eller indata förbrukas, anses det aktuella sammanlagda värdet vara det slutliga resultatet för den sista gruppen.
Ett sätt att ordna data som Stream Aggregate-algoritmen behöver är att få den förbeställd från ett index. Du måste definiera indexet med gruppuppsättningens kolumner som nycklar – i valfri ordning bland dem. Du vill också att indexet ska vara täckande. Tänk till exempel på följande fråga (vi kallar den fråga 1):
SELECT shipperid, MAX(orderdate) AS maxorderid FROM dbo.Orders GROUP BY shipperid;
Ett optimalt radlagerindex för att stödja denna fråga skulle vara ett som definieras med shipperid som den ledande nyckelkolumnen och orderdatum antingen som en inkluderad kolumn eller som en andra nyckelkolumn:
CREATE INDEX idx_sid_od ON dbo.Orders(shipperid, orderdate);
Med detta index på plats får du den uppskattade planen som visas i figur 1 (med SentryOne Plan Explorer).

Figur 1:Plan för fråga 1
Lägg märke till att Index Scan-operatorn har en Ordered:True-egenskap som anger att den krävs för att leverera raderna sorterade efter indexnyckeln. Operatören Stream Aggregate matar sedan in raderna ordnade som den behöver. När det gäller hur operatörens kostnad beräknas; innan vi kommer till det, ett snabbt förord först...
Som du kanske redan vet, när SQL Server optimerar en fråga, utvärderar den flera kandidatplaner och väljer så småningom den som har den lägsta uppskattade kostnaden. Den beräknade plankostnaden är summan av alla operatörernas beräknade kostnader. Varje operatörs uppskattade kostnad är i sin tur summan av den uppskattade I/O-kostnaden och den uppskattade CPU-kostnaden. Kostnadsenheten är meningslös i sin egen rätt. Dess relevans ligger i den jämförelse som optimeraren gör mellan kandidatplaner. Det vill säga att kalkylformlerna utformades med målet att mellan kandidatplanerna kommer den med lägst kostnad (förhoppningsvis) att representera den som kommer att slutföras snabbare. En fruktansvärt komplex uppgift att göra exakt!
Ju mer kostnadsformlerna tar tillräcklig hänsyn till de faktorer som verkligen påverkar algoritmens prestanda och skalning, desto mer exakta är de, och desto mer sannolikt är det att givet korrekta kardinalitetsuppskattningar kommer optimeraren att välja den optimala planen. Hur som helst, om du vill förstå varför optimeraren väljer en algoritm jämfört med en annan måste du förstå två huvudsakliga saker:en är hur algoritmerna fungerar och skalas, och en annan är SQL Servers kostnadsmodell.
Så tillbaka till planen i figur 1; låt oss försöka förstå hur kostnaderna beräknas. Som policy kommer Microsoft inte att avslöja de interna kostnadsformlerna som de använder. När jag var liten var jag fascinerad av att ta isär saker. Klockor, radioapparater, kassettband (ja, jag är så gammal), you name it. Jag ville veta hur saker gjordes. På samma sätt ser jag värde i att omvända formlerna eftersom om jag lyckas förutsäga kostnaden någorlunda exakt, betyder det förmodligen att jag förstår algoritmen väl. Under processen får du lära dig mycket.
Vår fråga tar in 1 000 000 rader. Även med detta antal rader verkar I/O-kostnaden vara försumbar jämfört med CPU-kostnaden, så det är förmodligen säkert att ignorera det.
När det gäller CPU-kostnaden vill du försöka ta reda på vilka faktorer som påverkar den och på vilket sätt. Teoretiskt kan det finnas ett antal faktorer:antal inmatningsrader, antal grupper, gruppuppsättningens kardinalitet, datatyp och storleken på gruppuppsättningens medlemmar. Så för att försöka mäta effekten av någon av dessa faktorer, vill du jämföra uppskattade kostnader för två frågor som endast skiljer sig åt i den faktor du vill mäta. Till exempel, för att mäta effekten av antalet rader på kostnaden, ha två frågor med olika antal inmatningsrader, men med alla andra aspekter desamma (antal grupper, gruppuppsättningens kardinalitet, etc.). Det är också viktigt att verifiera att de uppskattade siffrorna – inte de faktiska – är de önskade eftersom optimeraren förlitar sig på de uppskattade siffrorna för att beräkna kostnader.
När du gör sådana jämförelser är det bra att ha tekniker som låter dig kontrollera de uppskattade siffrorna helt. Ett enkelt sätt att kontrollera det uppskattade antalet inmatningsrader är till exempel att fråga ett tabelluttryck som är baserat på en TOP-fråga och tillämpa aggregatfunktionen i den yttre frågan. Om du är orolig för att optimeraren på grund av din användning av TOP-operatören kommer att tillämpa radmål och att dessa kommer att resultera i justering av de ursprungliga kostnaderna, gäller detta endast operatörer som visas i planen under Top-operatören (till höger), inte ovanför (till vänster). Operatören Stream Aggregate visas naturligtvis ovanför Top-operatorn i planen eftersom den matar in de filtrerade raderna.
När det gäller att kontrollera det uppskattade antalet utdatagrupper kan du göra det genom att använda grupperingsuttrycket
För att se till att du får Stream Aggregate-algoritmen och en serieplan kan du tvinga fram detta med frågetipsen:OPTION(ORDER GROUP, MAXDOP 1).
Du vill också ta reda på om det finns någon startkostnad för operatören så att du kan ta hänsyn till det i din omvända design.
Låt oss börja med att ta reda på hur antalet inmatningsrader påverkar operatörens beräknade CPU-kostnad. Självklart bör denna faktor vara relevant för operatörens kostnad. Dessutom kan du förvänta dig att kostnaden per rad är konstant. Här är ett par frågor för jämförelse som bara skiljer sig i det uppskattade antalet inmatningsrader (kalla dem Query 2 respektive Query 3):
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1); SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (200000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1);
Figur 2 har de relevanta delarna av de uppskattade planerna för dessa frågor:

Figur 2:Planer för fråga 2 och fråga 3
Om du antar att kostnaden per rad är konstant kan du beräkna den som skillnaden mellan operatörskostnaderna dividerat med skillnaden mellan operatörens indatakardinaliteter:
CPU cost per row = (0.125 - 0.065) / (200000 - 100000) = 0.0000006
För att verifiera att siffran du fick verkligen är konstant och korrekt kan du försöka förutsäga de uppskattade kostnaderna i frågor med andra antal inmatningsrader. Till exempel är den beräknade kostnaden med 500 000 inmatningsrader:
Cost for 500K input rows = <cost for 100K input rows> + 400000 * 0.0000006 = 0.065 + 0.24 = 0.305
Använd följande fråga för att kontrollera om din förutsägelse är korrekt (kalla den Fråga 4):
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (500000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1);
Den relevanta delen av planen för denna fråga visas i figur 3.
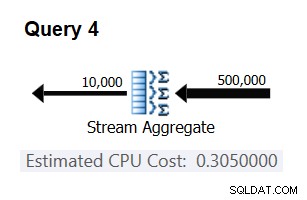
Figur 3:Plan för fråga 4
Bingo. Naturligtvis är det en bra idé att kontrollera flera ytterligare indatakardinaliteter. Med alla de jag kontrollerade var tesen att det finns en konstant kostnad per inmatningsrad på 0,0000006 korrekt.
Låt oss sedan försöka ta reda på hur det uppskattade antalet grupper påverkar operatörens CPU-kostnad. Du förväntar dig att det behövs en del CPU-arbete för att bearbeta varje grupp, och det är också rimligt att förvänta sig att det är konstant per grupp. För att testa den här avhandlingen och beräkna kostnaden per grupp kan du använda följande två frågor, som endast skiljer sig åt i antalet resultatgrupper (kalla dem Query 5 respektive Query 6):
SELECT orderid % 10000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 10000 OPTION(ORDER GROUP, MAXDOP 1); SELECT orderid % 20000 AS grp, MAX(orderdate) AS maxod FROM (SELECT TOP (100000) * FROM dbo.Orders) AS D GROUP BY orderid % 20000 OPTION(ORDER GROUP, MAXDOP 1);
De relevanta delarna av de uppskattade frågeplanerna visas i figur 4.
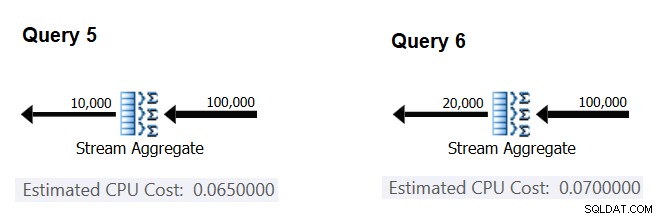
Figur 4:Planer för fråga 5 och fråga 6
På samma sätt som du beräknade den fasta kostnaden per ingångsrad, kan du beräkna den fasta kostnaden per utdatagrupp som skillnaden mellan operatörskostnaderna dividerat med skillnaden mellan operatörens utdatakardinaliteter:
CPU cost per group = (0.07 - 0.065) / (20000 - 10000) = 0.0000005
Och precis som jag visade tidigare kan du verifiera dina resultat genom att förutsäga kostnaderna med andra antal utdatagrupper och jämföra dina förutspådda siffror med de som produceras av optimeraren. Med alla antal grupper som jag försökte, var de förutspådda kostnaderna korrekta.
Med liknande tekniker kan du kontrollera om andra faktorer påverkar operatörens kostnad. Mina tester visar att grupperingsuppsättningens kardinalitet (antal uttryck som du grupperar efter), datatyperna och storlekarna för de grupperade uttrycken inte har någon inverkan på den uppskattade kostnaden.
Det som återstår är att kontrollera om det finns någon meningsfull startkostnad för operatören. Om det finns en sådan bör den fullständiga (förhoppningsvis) formeln för att beräkna operatörens CPU-kostnad vara:
Operator CPU cost = <startup cost> + <#input rows> * 0.0000006 + <#output groups> * 0.0000005
Så du kan härleda startkostnaden från resten:
Startup cost =- (<#input rows> * 0.0000006 + <#output groups> * 0.0000005)
Du kan använda vilken frågeplan som helst från den här artikeln för detta ändamål. Om du till exempel använder siffrorna från planen för fråga 5 som visas tidigare i figur 4 får du:
Startup cost = 0.065 - (100000 * 0.0000006 + 10000 * 0.0000005) = 0
Som det verkar har Stream Aggregate-operatören ingen CPU-relaterad startkostnad, eller så är den så låg att den inte visas med kostnadsmåttets precision.
Sammanfattningsvis är den omvända formeln för Stream Aggregate-operatörskostnaden:
I/O cost: negligible CPU cost: <#input rows> * 0.0000006 + <#output groups> * 0.0000005
Figur 5 visar skalningen av Stream Aggregate-operatörens kostnad med avseende på både antalet rader och antalet grupper.
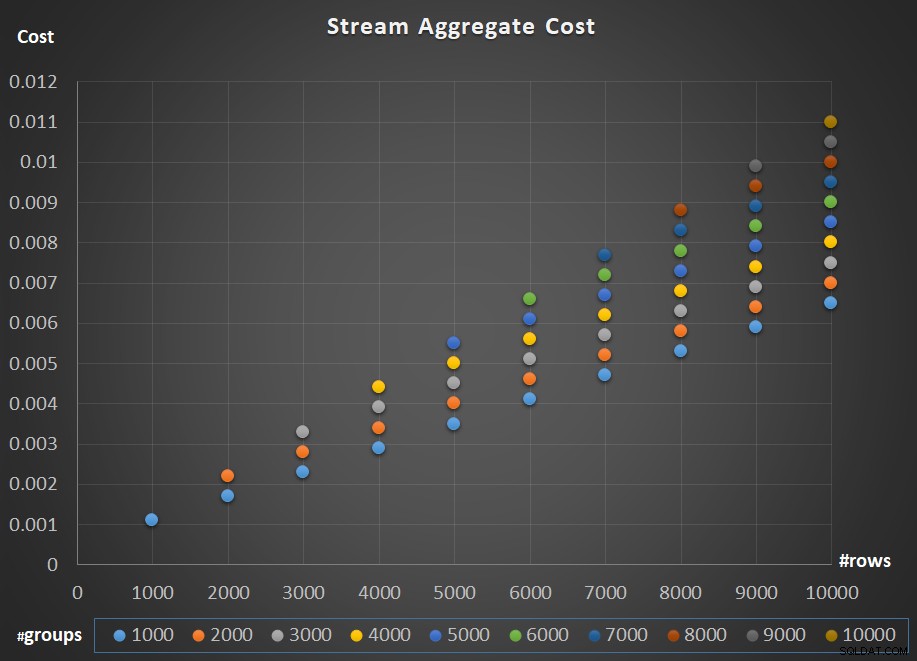
Figur 5:Skalningsdiagram för Stream Aggregate Algoritm
När det gäller operatörens skalning; det är linjärt. I de fall antalet grupper tenderar att vara proportionellt mot antalet rader ökar hela operatörens kostnad med samma faktor som både antalet rader och grupper ökar. Det betyder att en fördubbling av antalet både inmatningsrader och inmatningsgrupper resulterar i att hela operatörens kostnad fördubblas. För att se varför, anta att vi representerar operatörens kostnad som:
r * 0.0000006 + g * 0.0000005
Om du ökar både antalet rader och antalet grupper med samma faktor p får du:
pr * 0.0000006 + pg * 0.0000005 = p * (r * 0.0000006 + g * 0.0000005)
Så om, för ett givet antal rader och grupper, kostnaden för Stream Aggregate-operatören är C, resulterar en ökning av både antalet rader och grupper med samma faktor p i en operatörskostnad på pC. Se om du kan verifiera detta genom att identifiera exempel i diagrammet i figur 5.
I de fall där antalet grupper förblir ganska stabilt även när antalet inmatningsrader växer, får du fortfarande linjär skalning. Du betraktar bara kostnaden förknippad med antalet grupper som en konstant. Det vill säga, om kostnaden för operatören för ett givet antal rader och grupper är C =G (kostnad förknippad med antal grupper) plus R (kostnad förknippad med antal rader), ökar bara antalet rader med en faktor på p resulterar i G + pR. I ett sådant fall är naturligtvis hela operatörens kostnad mindre än pc. Det vill säga att dubbla antalet rader resulterar i mindre än en fördubbling av hela operatörens kostnad.
I praktiken, i många fall när du grupperar data, är antalet inmatningsrader betydligt större än antalet utdatagrupper. Detta faktum, i kombination med att den allokerade kostnaden per rad och kostnaden per grupp är nästan densamma, blir den del av operatörens kostnad som hänförs till antalet grupper försumbar. Som ett exempel, se planen för fråga 1 som visas tidigare i figur 1. I sådana fall är det säkert att bara tänka på operatörens kostnad som att bara skala linjärt med avseende på antalet inmatningsrader.
Specialfall
Det finns speciella fall där Stream Aggregate-operatören inte behöver sortera data alls. Om du tänker på det, har Stream Aggregate-algoritmen ett mer avslappnat ordningskrav från ingången jämfört med när du behöver data beställda för presentationsändamål, t.ex. när frågan har en yttre presentation ORDER BY-klausul. Stream Aggregate-algoritmen behöver helt enkelt alla rader från samma grupp ordnas tillsammans. Ta ingångsuppsättningen {5, 1, 5, 2, 1, 2}. För presentationsbeställningsändamål måste denna uppsättning ordnas på följande sätt:1, 1, 2, 2, 5, 5. För aggregeringsändamål skulle Stream Aggregate-algoritmen fortfarande fungera bra om data var ordnade i följande ordning:5, 5, 1, 1, 2, 2. Med detta i åtanke, när du beräknar ett skalärt aggregat (fråga med en aggregatfunktion och ingen GROUP BY-sats), eller grupperar data efter en tom grupperingsuppsättning, finns det aldrig mer än en grupp . Oberoende av ordningen på inmatningsraderna kan Stream Aggregate-algoritmen tillämpas. Algoritmen för hashaggregat hashasar data baserat på grupperingsuppsättningens uttryck som indata, och både med skalära aggregat och med en tom grupperingsuppsättning finns det inga indata att hasha efter. Så, både med skalära aggregat och med aggregat som tillämpas på en tom grupperingsuppsättning, använder optimeraren alltid Stream Aggregate-algoritmen, utan att data behöver förbeställas. Det är åtminstone fallet i radkörningsläge, eftersom för närvarande (från och med SQL Server 2017 CU4) batchläge endast är tillgängligt med Hash Aggregate-algoritmen. Jag kommer att använda följande två frågor för att demonstrera detta (kalla dem Fråga 7 och Fråga 8):
SELECT COUNT(*) AS numrows FROM dbo.Orders; SELECT COUNT(*) AS numrows FROM dbo.Orders GROUP BY ();
Planerna för dessa frågor visas i figur 6.
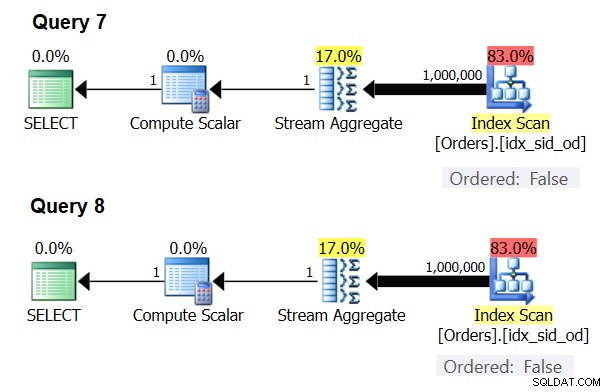
Figur 6:Planer för fråga 7 och fråga 8
Försök att tvinga fram en Hash Aggregate-algoritm i båda fallen:
SELECT COUNT(*) AS numrows FROM dbo.Orders OPTION(HASH GROUP); SELECT COUNT(*) AS numrows FROM dbo.Orders GROUP BY () OPTION(HASH GROUP);
Optimeraren ignorerar din begäran och producerar samma planer som visas i figur 6.
Snabbfrågesport:vad är skillnaden mellan ett skalärt aggregat och ett aggregat som tillämpas på en tom grupperingsuppsättning?
Svar:med en tom inmatningsuppsättning returnerar ett skalärt aggregat ett resultat med en rad, medan ett aggregat i en fråga med en tom grupperingsuppsättning returnerar en tom resultatuppsättning. Prova det:
SELECT COUNT(*) AS numrows FROM dbo.Orders WHERE 1 = 2;
numrows ----------- 0 (1 row affected)
SELECT COUNT(*) AS numrows FROM dbo.Orders WHERE 1 = 2 GROUP BY ();
numrows ----------- (0 rows affected)
När du är klar, kör följande kod för rengöring:
DROP INDEX idx_sid_od ON dbo.Orders;
Sammanfattning och utmaning
Att omvända kostnadsformeln för Stream Aggregate-algoritmen är en barnlek. Jag kunde bara ha berättat att kostnadsformeln för en förbeställd Stream Aggregate-algoritm är @numrows * 0,0000006 + @numgroups * 0,0000005 istället för en hel artikel för att förklara hur du räknar ut detta. Poängen var dock att beskriva processen och principerna för reverse-engineering, innan man går vidare till de mer komplexa algoritmerna och tröskelvärdena där en algoritm blir mer optimal än de andra. Lär dig att fiska istället för att ge dig fisk typ. Jag har lärt mig så mycket och upptäckt saker som jag inte ens tänkt på, medan jag försökte omvända kostnadsformler för olika algoritmer.
Är du redo att testa dina kunskaper? Ditt uppdrag, om du väljer att acceptera det, är ett snäpp svårare än att bakåtkonstruera Stream Aggregate-operatören. Reverse-engineera kostnadsformeln för en seriell sorteringsoperatör. Detta är viktigt för vår forskning eftersom en Stream Aggregate-algoritm som används för en fråga med en icke-tom grupperingsuppsättning, där indata inte är förbeställda, kräver explicit sortering. I ett sådant fall beror kostnaden och skalningen för den aggregerade operationen på kostnaden och skalningen för Sorterings- och Stream Aggregate-operatörerna tillsammans.
Om du lyckas komma anständigt nära med att förutsäga kostnaden för sorteringsoperatören, kan du känna att du förtjänat rätten att lägga till din signatur "Reverse Engineer". Det finns många mjukvaruingenjörer där ute; men du ser verkligen inte många omvänd ingenjörer! Se bara till att testa din formel både med små siffror och med stora; du kanske blir förvånad över vad du hittar.
