Hur lagrar man dubbelriktade relationer i ett RDBMS som MySQL?

Så här kommer dessa två tillvägagångssätt att representeras fysiskt i databasen:

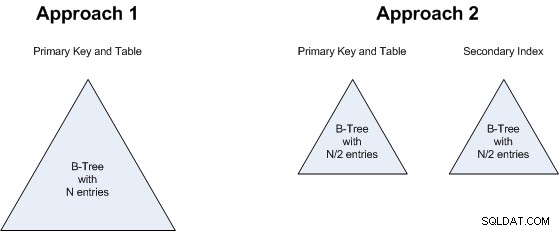
Låt oss analysera båda tillvägagångssätten...

Tillvägagångssätt 1 (båda riktningarna lagrade i tabellen):

• PRO:Enklare frågor.
• CON:Data kan skadas genom att infoga/uppdatera/ta bort endast en riktning.
• MINOR PRO:Kräver inga ytterligare begränsningar för att säkerställa att en vänskap inte kan dupliceras.
• Ytterligare analys behövs:
  1. TIE:Ett index omslag båda riktningarna, så du behöver inte ett sekundärt index.
  2. TIE:Lagringskrav.
  3. TIE:Prestanda.

Tillvägagångssätt 2 (endast en riktning lagrad i tabellen):

• CON:Mer komplicerade frågor.
• PRO:Kan inte korrumpera data genom att glömma att hantera den motsatta riktningen, eftersom det inte finns någon motsatt riktning .
• MINOR CON:Kräver CHECK(UID < FriendID) , så samma vänskap kan aldrig representeras på två olika sätt, och nyckeln på (UID, FriendID) kan göra sitt jobb.
• Ytterligare analys behövs:
  1. TIE:Två index krävs för att täcka båda riktningarna för förfrågning (sammansatt index på {UID, FriendID} och sammansatt index på {FriendID, UID} ).
  2. TIE:Lagringskrav.
  3. TIE:Prestanda.

punkt 1 är av särskilt intresse. MySQL/InnoDB alltid kluster data, och sekundära index kan vara dyra i klustrade tabeller (se "Nackdelar med klustring" i denna artikel ), så det kan tyckas som om det sekundära indexet i tillvägagångssätt 2 skulle äta upp alla fördelarna med färre rader. Men , innehåller det sekundära indexet exakt samma fält som det primära (endast i motsatt ordning) så det finns ingen lagringskostnad i det här specifika fallet. Det finns inte heller någon pekare till tabellhög (eftersom det inte finns någon tabellhög), så det är förmodligen ännu billigare lagringsmässigt än ett normalt heapbaserat index. Och förutsatt att frågan täcks av indexet, kommer det inte att finnas en dubbelsökning som normalt är associerad med ett sekundärt index i en klustrad tabell heller. Så detta är i princip oavgjort (varken tillvägagångssätt 1 eller tillvägagångssätt 2 har betydande fördelar).

punkt 2 är relaterat till punkt 1:det spelar ingen roll om vi kommer att ha ett B-träd med N-värden eller två B-träd, var och en med N/2-värden. Så detta är också oavgjort:båda metoderna kommer att använda ungefär samma mängd lagringsutrymme.

Samma resonemang gäller för punkt 3 :om vi söker efter ett större B-träd eller två mindre spelar ingen större roll, så detta är också oavgjort.

Så, för robusthetens skull, och trots något fulare frågor och ett behov av ytterligare CHECK , jag skulle gå med tillvägagångssätt 2.