Förra månaden täckte jag Peter Larssons pussel om att matcha utbud med efterfrågan. Jag visade Peters enkla markörbaserade lösning och förklarade att den har linjär skalning. Utmaningen jag lämnade dig med är att försöka komma på en uppsättningsbaserad lösning på uppgiften, och pojke, har folk tagit sig an utmaningen! Tack Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie och, naturligtvis, Peter Larsson, för att du skickade dina lösningar. Några av idéerna var briljanta och direkt häpnadsväckande.
Den här månaden ska jag börja utforska de inskickade lösningarna, ungefär, från de sämst presterande till de bäst presterande. Varför ens bry sig om de dåligt presterande? För du kan fortfarande lära dig mycket av dem; till exempel genom att identifiera antimönster. Faktum är att det första försöket att lösa denna utmaning för många människor, inklusive mig själv och Peter, är baserat på ett intervallkorsningskoncept. Det råkar vara så att den klassiska predikatbaserade tekniken för att identifiera intervallskärningar har dålig prestanda eftersom det inte finns något bra indexeringsschema som stödjer det. Den här artikeln är tillägnad detta dåliga resultat. Trots den dåliga prestandan är det en intressant övning att arbeta med lösningen. Det kräver att man tränar på skickligheten att modellera problemet på ett sätt som lämpar sig för uppsättningsbaserad behandling. Det är också intressant att identifiera orsaken till den dåliga prestandan, vilket gör det lättare att undvika anti-mönstret i framtiden. Kom ihåg att den här lösningen bara är utgångspunkten.
DDL och en liten uppsättning exempeldata
Som en påminnelse innebär uppgiften att fråga efter en tabell som heter "Auktioner." Använd följande kod för att skapa tabellen och fylla i den med en liten uppsättning exempeldata:
SLÄPP TABELL OM FINNS dbo.Auktioner; CREATE TABLE dbo.Auctions( ID INT NOT NULL IDENTITY(1, 1) CONSTRAINT pk_Auctions PRIMARY KEY CLUSTERED, Code CHAR(1) NOT NULL CONSTRAINT ck_Auctions_Code CHECK (Code ='D' OR Code ='S'), Quantity (19 DECIMAL , 6) NOT NULL CONSTRAINT ck_Auctions_Quantity CHECK (Quantity> 0)); STÄLL IN ANTALT PÅ; RADERA FRÅN dbo.Auktioner; SET IDENTITY_INSERT dbo.Auktioner PÅ; INSERT INTO dbo.Auctions(ID, Code, Quantity) VÄRDEN (1, 'D', 5.0), (2, 'D', 3.0), (3, 'D', 8.0), (5, 'D', 2.0), (6, 'D', 8.0), (7, 'D', 4.0), (8, 'D', 2.0), (1000, 'S', 8.0), (2000, 'S', 6.0), (3000, 'S', 2.0), (4000, 'S', 2.0), (5000, 'S', 4.0), (6000, 'S', 3.0), (7000, 'S', 2,0); SET IDENTITY_INSERT dbo.Auktioner AV;
Din uppgift var att skapa parningar som matchar utbud och efterfrågeposter baserat på ID-beställning, skriva dessa till en tillfällig tabell. Följande är det önskade resultatet för den lilla uppsättningen exempeldata:
DemandID SupplyID TradeQuantity-----------------------------------------------------1 1000 5,0000002 1000 3,0000003 2000 6,0000003 3000 2,0000005 4000 2,0000006 5000 4,0000006 6000 3,0000006 7000 1,0000007 7000 1,000000
Förra månaden tillhandahöll jag också kod som du kan använda för att fylla i auktionstabellen med en stor uppsättning exempeldata, som kontrollerar antalet poster för utbud och efterfrågan samt deras kvantitetsutbud. Se till att du använder koden från förra månadens artikel för att kontrollera lösningarnas prestanda.
Modellera data som intervall
En spännande idé som lämpar sig för att stödja uppsättningsbaserade lösningar är att modellera data som intervall. Med andra ord, representera varje efterfråge- och utbudspost som ett intervall som börjar med löpande totala kvantiteter av samma slag (efterfrågan eller utbud) upp till men exklusive strömmen, och slutar med löpande summa inklusive strömmen, naturligtvis baserat på ID beställning. Om man till exempel tittar på den lilla uppsättningen exempeldata, är den första efterfrågeposten (ID 1) för en kvantitet av 5,0 och den andra (ID 2) för en kvantitet av 3,0. Den första efterfrågeposten kan representeras med intervallstart:0,0, slut:5,0, och den andra med intervallstart:5,0, slut:8,0, och så vidare.
På liknande sätt, den första utbudsposten (ID 1000) är för en kvantitet av 8,0 och den andra (ID 2000) är för en kvantitet av 6,0. Den första leveransposten kan representeras med intervallstart:0,0, slut:8,0 och den andra med intervallstart:8,0, slut:14,0, och så vidare.
De efterfråge-utbuds-parningar du behöver skapa är sedan de överlappande segmenten av de skärande intervallen mellan de två typerna.
Detta förstås förmodligen bäst med en visuell skildring av den intervallbaserade modelleringen av data och det önskade resultatet, som visas i figur 1.
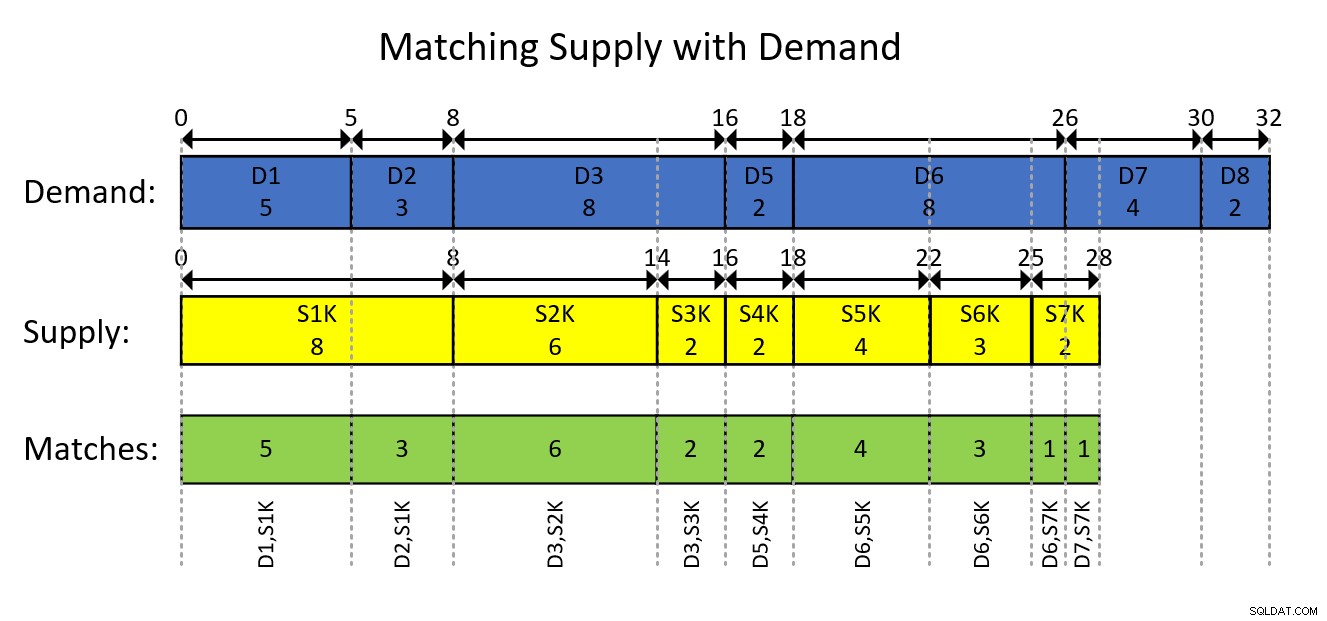Figur 1:Modellera data som intervall
Den visuella avbildningen i figur 1 är ganska självförklarande men kortfattat...
De blå rektanglarna representerar efterfrågeposterna som intervall, och visar de exklusiva löpande totala kvantiteterna som början av intervallet och den inklusive löpande summan som slutet av intervallet. De gula rektanglarna gör samma sak för leveransposter. Lägg sedan märke till hur de överlappande segmenten av de skärande intervallen av de två typerna, som avbildas av de gröna rektanglarna, är de efterfråge-utbudsparningar du behöver för att producera. Till exempel är den första resultatparningen med efterfråge-ID 1, utbuds-ID 1000, kvantitet 5. Den andra resultatparningen är med efterfråge-ID 2, utbuds-ID 1000, kvantitet 3. Och så vidare.
Intervallkorsningar med CTE
Innan du börjar skriva T-SQL-koden med lösningar baserade på intervallmodelleringsidén bör du redan ha en intuitiv känsla för vilka index som troligen kommer att vara användbara här. Eftersom du sannolikt kommer att använda fönsterfunktioner för att beräkna löpande summor, kan du dra nytta av ett täckande index med en nyckel baserad på kolumnerna Kod, ID och inklusive kolumnen Kvantitet. Här är koden för att skapa ett sådant index:
SKAPA UNIKT INKLUSTERAT INDEX idx_Code_ID_i_Quantity PÅ dbo.Auctions(Code, ID) INCLUDE(Quantity);
Det är samma index som jag rekommenderade för den markörbaserade lösningen som jag täckte förra månaden.
Här finns också potential att dra nytta av batchbearbetning. Du kan aktivera dess övervägande utan kraven för batchläge på rowstore, t.ex. med SQL Server 2019 Enterprise eller senare, genom att skapa följande dummy columnstore-index:
SKAPA ICKE CLUSTERED COLUMNSTORE INDEX idx_cs PÅ dbo.Auctions(ID) WHERE ID =-1 OCH ID =-2;
Du kan nu börja arbeta med lösningens T-SQL-kod.
Följande kod skapar intervallen som representerar efterfrågeposterna:
WITH D0 AS-- D0 beräknar löpande efterfrågan som EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extraherar föregående EndDemand som StartDemand, uttrycker start-end-efterfrågan som ett intervallD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0)SELECT *FROM D;
Frågan som definierar CTE D0 filtrerar efterfrågeposter från auktionstabellen och beräknar en löpande total kvantitet som slutavgränsare för efterfrågeintervallen. Sedan frågar frågan som definierar den andra CTE:n D frågar D0 och beräknar startavgränsaren för efterfrågeintervallen genom att subtrahera den aktuella kvantiteten från slutavgränsaren.
Denna kod genererar följande utdata:
ID Kvantitet StartDemand EndDemand---- ---------- ------------ ----------1 5,000000 0,000000 5,0000002 3,000000 5,000000 8,0000003 8,000000 8,000000 16,0000005 2,000000 16,000000 18,0000006 8,000000 18,000000 26,0000007 4,000000 26,0000 3,000 000 26,000Försörjningsintervallen genereras mycket lika genom att tillämpa samma logik på försörjningsposterna, med hjälp av följande kod:
WITH S0 AS-- S0 beräknar körande utbud som EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S extraherar föregående EndSupply som StartSupply, uttrycker start-end utbud som ett intervallS AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)SELECT *FROM S;Denna kod genererar följande utdata:
ID Kvantitet StartSupply EndSupply----- ---------- ------------ ----------1000 8,000000 0,000000 8,0000002000 6,000000 8,000000 14,0000003000 2.000000 14.000000 16.0000004000 2.000000 16.000000 18.0000005000 4.000000 18.000000 22.0000006000 3.000000 22.000000 25.0000007000 2.000000 25.0000 27.000000Vad som återstår är sedan att identifiera de korsande efterfråge- och utbudsintervallen från CTE:erna D och S, och beräkna de överlappande segmenten av dessa skärande intervall. Kom ihåg att resultatparningarna ska skrivas in i en tillfällig tabell. Detta kan göras med följande kod:
-- Släpp temp tabell om det finns DROP TABLE OM FINNS #MyPairings; WITH D0 AS-- D0 beräknar löpande efterfrågan som EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extraherar föregående EndDemand som StartDemand, uttrycker efterfrågan från början som ett intervallD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0),S0 AS-- S0 beräknar löpande utbud som EndSupply( SELECT ID, Quantity, SUM(Quantity) ÖVER (ORDNING EFTER ID-RADER OBEGRÄNSAD FÖREGÅENDE) SOM EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S-utdrag föregående EndSupply som StartSupply, uttrycker start-end-tillförsel som ett intervall AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)-- Yttre fråga identifierar affärer som de överlappande segmenten av de skärande intervallen-- I de korsande efterfråge- och utbudsintervallen är handelsmängden då -- MINST(EndDemand, EndSupply) - GREATEST(StartDemsnad, StartSupply)SELECT D.ID AS DemandID, S.ID AS SupplyID, CASE WH SV EndDemandStartSupply THEN StartDemand ELSE StartSupply END AS TradeQuantityINTO #MyPairingsFROM D INNER JOIN S ON D.StartDemand S.Demand> S. Förutom koden som skapar efterfråge- och utbudsintervallen, som du redan såg tidigare, är huvudtillägget här den yttre frågan, som identifierar de skärande intervallen mellan D och S, och beräknar de överlappande segmenten. För att identifiera de skärande intervallen sammanfogar den yttre frågan D och S med hjälp av följande joinpredikat:
D.StartDemandS.StartSupply Det är det klassiska predikatet för att identifiera intervallskärning. Det är också huvudkällan till lösningens dåliga prestanda, som jag ska förklara snart.
Den yttre frågan beräknar också handelskvantiteten i SELECT-listan som:
MINST(EndDemand, EndSupply) - GREATEST(StartDemand, StartSupply)Om du använder Azure SQL kan du använda det här uttrycket. Om du använder SQL Server 2019 eller tidigare kan du använda följande logiskt likvärdiga alternativ:
CASE WHEN EndDemandStartSupply THEN StartDemand ELSE StartSupply END Eftersom kravet var att skriva resultatet i en temporär tabell, använder den yttre frågan en SELECT INTO-sats för att uppnå detta.
Idén att modellera data som intervall är helt klart spännande och elegant. Men hur är det med prestanda? Tyvärr har denna specifika lösning ett stort problem relaterat till hur intervallkorsning identifieras. Undersök planen för denna lösning som visas i figur 2.
Figur 2:Frågeplan för korsningar med CTE-lösning
Låt oss börja med de billiga delarna av planen.
Den yttre ingången för den kapslade slingan beräknar behovsintervallen. Den använder en Index Seek-operator för att hämta efterfrågeposterna och en batch-läge Window Aggregate-operator för att beräkna efterfrågeintervallets slutavgränsare (kallad Expr1005 i denna plan). Efterfrågan intervall startavgränsare är då Expr1005 – Kvantitet (från D).
Som en sidoanteckning kan du tycka att användningen av en explicit sorteringsoperator före batchläget Window Aggregate-operator är överraskande här, eftersom efterfrågeposterna som hämtas från Indexsökningen redan är sorterade efter ID som fönsterfunktionen behöver vara. Detta har att göra med det faktum att SQL Server för närvarande inte stöder en effektiv kombination av parallell orderbevarande indexoperation före en parallell batchläge Window Aggregate-operator. Om du tvingar fram en serieplan bara för experimentändamål kommer du att se sorteringsoperatorn försvinna. SQL Server bestämde överlag, användningen av parallellism här var att föredra, trots att det resulterade i den extra explicita sorteringen. Men återigen, den här delen av planen representerar en liten del av arbetet i det stora hela.
På liknande sätt börjar den inre ingången för Nested Loops-kopplingen med att beräkna matningsintervallen. Märkligt nog valde SQL Server att använda radlägesoperatorer för att hantera denna del. Å ena sidan innebär radlägesoperatorer som används för att beräkna löpande summor mer overhead än batchläget Window Aggregate-alternativet; å andra sidan har SQL Server en effektiv parallell implementering av en orderbevarande indexoperation som följer av fönsterfunktionens beräkning, och undviker explicit sortering för denna del. Det är konstigt att optimeraren valde en strategi för efterfrågeintervallen och en annan för utbudsintervallen. I vilket fall som helst hämtar Indexsök-operatören leveransposterna, och den efterföljande sekvensen av operatörer fram till Compute Scalar-operatören beräknar leveransintervallets slutavgränsare (refererad till som Expr1009 i denna plan). Tillgångsintervallets startavgränsare är då Expr1009 – Kvantitet (från S).
Trots mängden text jag använde för att beskriva dessa två delar, är den verkligt dyra delen av arbetet i planen det som kommer härnäst.
Nästa del måste sammanfoga efterfrågeintervallen och utbudsintervallen med hjälp av följande predikat:
D.StartDemandS.StartSupply Utan något stödjande index, om man antar DI-efterfrågeintervall och SI-tillförselintervall, skulle detta innebära bearbetning av DI * SI-rader. Planen i figur 2 skapades efter att ha fyllt auktionstabellen med 400 000 rader (200 000 efterfrågeposter och 200 000 utbudsposter). Så, utan något stödjande index, skulle planen ha behövt bearbeta 200 000 * 200 000 =40 000 000 000 rader. För att minska denna kostnad valde optimeraren att skapa ett temporärt index (se Index Spool-operatören) med leveransintervallets slutavgränsare (Expr1009) som nyckel. Det är i stort sett det bästa man kan göra. Detta tar dock bara hand om en del av problemet. Med två intervallpredikat kan endast ett stödjas av ett indexsökpredikat. Den andra måste hanteras med ett restpredikat. Du kan faktiskt se i planen att sökningen i det tillfälliga indexet använder sökpredikatet Expr1009> Expr1005 – D.Quantity, följt av en filteroperator som hanterar restpredikatet Expr1005> Expr1009 – S.Quantity.
Om man antar att sökpredikatet i genomsnitt isolerar hälften av utbudsraderna från indexet per efterfrågerad, är det totala antalet rader som sänds ut från Index Spool-operatören och behandlas av Filter-operatören då DI * SI / 2. I vårt fall, med 200 000 efterfrågerader och 200 000 utbudsrader, översätts detta till 20 000 000 000. Faktum är att pilen som går från Index Spool-operatorn till Filter-operatorn rapporterar ett antal rader nära detta.
Den här planen har kvadratisk skalning, jämfört med den linjära skalningen av den markörbaserade lösningen från förra månaden. Du kan se resultatet av ett prestandatest som jämför de två lösningarna i figur 3. Du kan tydligt se den snyggt formade parabeln för den setbaserade lösningen.
Figur 3:Utförande av korsningar med CTE Lösning kontra markörbaserad lösning
Intervallkorsningar med hjälp av tillfälliga tabeller
Du kan förbättra saker och ting något genom att ersätta användningen av CTE:er för efterfråge- och utbudsintervall med tillfälliga tabeller, och för att undvika indexspolen, skapa ditt eget index på temptabellen som håller utbudsintervallen med slutavgränsaren som nyckel. Här är den fullständiga lösningens kod:
-- Släpp temporära tabeller om det finns DROP TABELL OM FINNS #MyPairings, #Demand, #Supply; WITH D0 AS-- D0 beräknar löpande efterfrågan som EndDemand( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extraherar föregående EndDemand som StartDemand, uttrycker start-end-efterfrågan som ett intervallD AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0)SELECT ID, Quantity, CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand, CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemandINTO #DemandFROM D;WITH S0 AS-- S0 beräknar körande utbud som EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S extraherar prev EndSupply som StartSupply, uttrycker start-end utbud som ett intervall AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)SELECT ID, Quantity, CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply, CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupplyINTO #SupplyFROM S; SKAPA UNIKT CLUSTERED INDEX idx_cl_ES_ID PÅ #Supply(EndSupply, ID); -- Yttre fråga identifierar affärer som de överlappande segmenten av de skärande intervallen-- I de korsande efterfråge- och utbudsintervallen är handelsmängden då -- MINST(EndDemand, EndSupply) - GREATEST(StartDemsnad, StartSupply)SELECT D.ID AS DemandID, S.ID SOM SupplyID, CASE NÄR EndDemandStartSupply THEN StartDemand ANDRA StartSupply ENDAS SOM TradeQuantityINTO #MyPairingsFROM #Demand AS D INNER JOIN #Supply AS SStarWITHEFOR S.StartSupply; Planerna för denna lösning visas i figur 4:
Figur 4:Frågeplan för korsningar med Temp-tabelllösning
De två första planerna använder en kombination av batch-mode Index Seek + Sort + Window Aggregate-operatorer för att beräkna utbuds- och efterfrågeintervall och skriva dem till tillfälliga tabeller. Den tredje planen hanterar indexskapandet på #Supply-tabellen med EndSupply-avgränsaren som ledande nyckel.
Den fjärde planen representerar överlägset huvuddelen av arbetet, med en Nested Loops join-operatör som matchar varje intervall från #Demand, de korsande intervallen från #Supply. Observera att även här förlitar sig Index Seek på predikatet #Supply.EndSupply> #Demand.StartDemand som sökpredikat och #Demand.EndDemand> #Supply.StartSupply som restpredikat. Så när det gäller komplexitet/skalning får du samma kvadratiska komplexitet som för den tidigare lösningen. Du betalar bara mindre per rad eftersom du använder ditt eget index istället för indexrullen som användes av den tidigare planen. Du kan se prestandan för den här lösningen jämfört med de två föregående i figur 5.
Figur 5:Prestanda för korsningar med hjälp av temporära tabeller jämfört med andra två lösningar
Som du kan se presterar lösningen med temp-tabellerna bättre än den med CTE:erna, men den har fortfarande kvadratisk skalning och går väldigt dåligt jämfört med markören.
Vad händer härnäst?
Den här artikeln täckte det första försöket att hantera den klassiska matchningsuppgiften utbud och efterfrågan med en uppsättningsbaserad lösning. Tanken var att modellera data som intervall, matcha utbud med efterfrågeposter genom att identifiera korsande utbuds- och efterfrågeintervall, och sedan beräkna handelskvantiteten baserat på storleken på de överlappande segmenten. Helt klart en spännande idé. Det största problemet med det är också det klassiska problemet med att identifiera intervallskärningar genom att använda två avståndspredikat. Även med det bästa indexet på plats kan du bara stödja ett intervallpredikat med en indexsökning; det andra intervallpredikatet måste hanteras med ett restpredikat. Detta resulterar i en plan med kvadratisk komplexitet.
Så vad kan du göra för att övervinna detta hinder? Det finns flera olika idéer. En briljant idé tillhör Joe Obbish, som du kan läsa om i detalj i hans blogginlägg. Jag kommer att täcka andra idéer i kommande artiklar i serien.
[ Hoppa till:Ursprunglig utmaning | Lösningar:Del 1 | Del 2 | Del 3 ]