Kapslade loopar och Performance Spools

Introduktion

Prestanda spolar är lata spolar som lagts till av optimeraren för att minska den uppskattade kostnaden för innersidan av kapslade loopar går med . De finns i tre varianter:Lazy Table Spool , Lazy Index Spool , och Lazy Row Count Spool . Ett exempel på planform som visar en prestationsspole för lat bord är nedan:

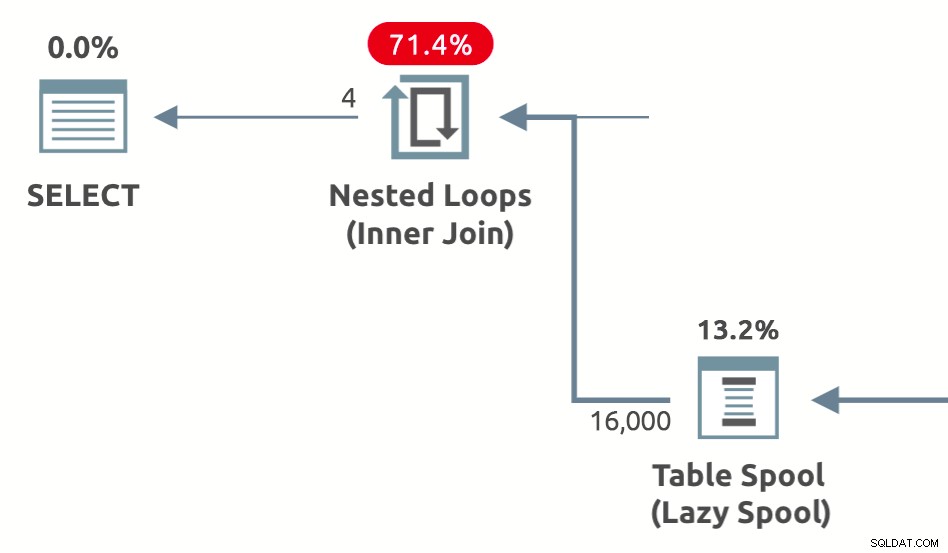
Frågorna jag tänkt besvara i den här artikeln är varför, hur och när frågeoptimeraren introducerar varje typ av prestandaspool.

Precis innan vi börjar vill jag betona en viktig punkt:Det finns två distinkta typer av kapslade slingkopplingar i utförandeplaner. Jag kommer att referera till sorten med yttre referenser som en ansökan , och typen med ett join-predikat på själva joinoperatorn som en kapslade loops join . För att vara tydlig handlar den här skillnaden om verkställandeplanoperatörer , inte T-SQL-frågesyntax. För mer information, se min länkade artikel.

Prestanda spolar

Bilden nedan visar prestationsspolen exekveringsplansoperatörer som visas i Plan Explorer (översta raden) och SSMS 18.3 (nedre raden):

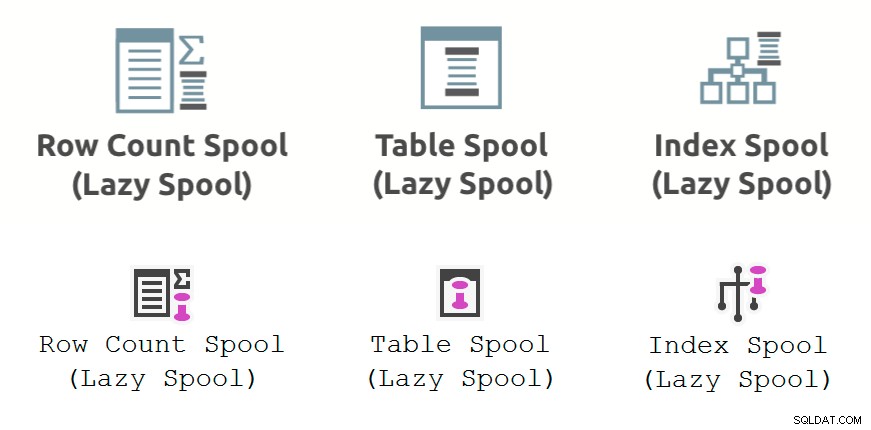
Allmänna kommentarer

Alla prestandaspolar är lata . Spolens arbetsbord fylls gradvis, en rad i taget, allteftersom rader strömmar genom spolen. (Ivriga spolar däremot förbrukar all input från sin underordnade operatör innan de returnerar några rader till sin förälder).

Prestandaspolar visas alltid på insidan (den lägre ingången i grafiska exekveringsplaner) för en kapslad loop-operator. Den allmänna idén är att cachelagra och spela upp resultat, vilket sparar upprepade körningar av interna operatörer där det är möjligt.

När en spool kan spela om cachade resultat kallas detta en spolning tillbaka . När spoolen måste köra sina underordnade operatörer för att få korrekt data, en återbindning inträffar.

Du kanske tycker det är bra att tänka på en spool rebind som en cachemiss och en spolning bakåt som en cacheträff.

Lazy Table Spool

Den här typen av prestationsspool kan användas med både apply och kapslade loopar går samman .

Ansök

En återbindning (cache miss) inträffar när en yttre referens värdeförändringar. En lat bordsspole binds igen genom att trunkera dess arbetstabell och fyller på den helt från dess underordnade operatörer.

En spolning bakåt (cacheträff) uppstår när den inre sidan körs med samma yttre referensvärden som de omedelbart föregående loop iteration. En bakåtspolning spelar upp cachade resultat från spolens arbetsbord, vilket sparar kostnaden för att köra om planoperatörerna under spolen.

Obs! En lazy table spool cachar bara resultat för en uppsättning apply yttre referens värden åt gången.

Inkapslade loopar gå med

Den lata bordsspolen fylls i en gång under den första loopiterationen. Spolen spolar tillbaka sitt innehåll för varje efterföljande iteration av sammanfogningen. Med kapslade slingor sammanfogning är insidan av sammanfogningen en statisk uppsättning rader eftersom sammanfogningspredikatet är på själva sammanfogningen. Den statiska raduppsättningen på insidan kan därför cachelagras och återanvändas flera gånger via spolen. En kapslad loop-join prestationsspool binds aldrig om.

Lazy Row Count Spool

En radräkningsspole är lite mer än en bordspole utan kolumner. Den cachar förekomsten av en rad, men projicerar inga kolumndata. Förutom att notera dess existens och nämna att det kan vara en indikation på ett fel i källfrågan, jag kommer inte att ha mer att säga om radräkningsspolar.

Från och med nu och framåt, när du ser "bordspole" i texten, läs det som "tabell (eller radantal) spole" eftersom de är så lika.

Lat Index Spool

Lazy Index Spool operatör är endast tillgänglig med applicera .

Indexspoolen upprätthåller en arbetstabell som inte är trunkerad när yttre referens värden förändras. Istället läggs ny data till den befintliga cachen, indexerad av de yttre referensvärdena. En lat indexspole skiljer sig från en lat bordsspole genom att den kan spela om resultat från alla föregående loop iteration, inte bara den senaste.

Nästa steg för att förstå när prestationsspolar visas i exekveringsplaner kräver att du förstår lite om hur optimeraren fungerar.

Optimizerbakgrund

En källfråga konverteras till en logisk trädrepresentation genom att analysera, algebrisera, förenkla och normalisera. När det resulterande trädet inte kvalificerar sig för en trivial plan, letar den kostnadsbaserade optimeraren efter logiska alternativ som garanterat ger samma resultat, men till en lägre uppskattad kostnad.

När optimeraren har genererat potentiella alternativ, implementerar den var och en med lämpliga fysiska operatörer och beräknar uppskattade kostnader. Den slutliga genomförandeplanen är byggd från det lägsta kostnadsalternativet som hittats för varje operatörsgrupp. Du kan läsa mer information om processen i min Query Optimizer Deep Dive-serie.

De allmänna villkoren som krävs för att en prestationsspool ska visas i optimerarens slutliga plan är:

Optimeraren måste utforska ett logiskt alternativ som inkluderar en logisk spool i ett genererat substitut. Det här är mer komplext än det låter, så jag kommer att packa upp detaljerna i nästa huvudavsnitt.
Den logiska spoolen måste vara implementerbar som en fysisk spole operatör i exekveringsmotorn. För moderna versioner av SQL Server betyder detta i huvudsak att alla nyckelkolumner i en indexspool måste vara jämförbara typ, inte mer än 900 byte* totalt, med 64 nyckelkolumner eller färre.
Det bästa komplett plan efter kostnadsbaserad optimering måste innehålla ett av spolalternativen. Med andra ord, alla kostnadsbaserade val som görs mellan spool- och icke-spool-alternativ måste komma ut till fördel för spolen.

_{* Detta värde är hårdkodat i SQL Server och har inte ändrats efter ökningen till 1700 byte för icke-klustrade indexnycklar från SQL Server 2016 och framåt. Detta beror på att spoolindexet är ett kluster index, inte ett icke-klustrat index.}

Optimeringsregler

Vi kan inte specificera en spool med T-SQL, så att få en i en exekveringsplan innebär att optimeraren måste välja att lägga till den. Som ett första steg innebär detta att optimeraren måste inkludera en logisk spole i ett av alternativen som den väljer att utforska.

Optimeraren tillämpar inte uttömmande alla logiska ekvivalensregler som den känner till på varje frågeträd. Detta skulle vara slösaktigt med tanke på optimerarens mål att snabbt ta fram en rimlig plan. Det finns flera aspekter av detta. Först fortsätter optimeraren i etapper, med billigare och oftare tillämpliga regler som testas först. Om en rimlig plan hittas i ett tidigt skede, eller om frågan inte kvalificerar sig för senare steg, kan optimeringsarbetet avslutas tidigt med den lägsta kostnadsplanen som hittats hittills. Den här strategin hjälper till att förhindra att spendera mer tid på optimering än vad som sparas genom inkrementella kostnadsförbättringar.

Regelmatchning

Varje logisk operator i frågeträdet kontrolleras snabbt för en mönstermatchning mot reglerna som är tillgängliga i det aktuella optimeringsstadiet. Till exempel kommer varje regel bara att matcha en delmängd av logiska operatorer och kan även kräva att specifika egenskaper finns på plats, till exempel garanterad sorterad indata. En regel kan matcha en individuell logisk operation (en enda grupp) eller flera sammanhängande grupper (ett underavsnitt av planen).

När den har matchats uppmanas en kandidatregel att generera ett löftesvärde . Detta är en siffra som representerar hur sannolikt den nuvarande regeln är att ge ett användbart resultat, givet det lokala sammanhanget. Till exempel kan en regel generera ett högre löftesvärde när målet har många dubbletter på sin inmatning, ett stort uppskattat antal rader, garanterat sorterad indata eller någon annan önskvärd egenskap.

När lovande utforskningsregler har identifierats, sorterar optimeraren dem i löftesvärdeordning och börjar be dem att generera nya logiska substitut. Varje regel kan generera en eller flera substitut som senare kommer att implementeras med hjälp av fysiska operatörer. Som en del av den processen beräknas en uppskattad kostnad.

Poängen med allt detta när det gäller prestationsspolar är att den logiska planformen och egenskaperna måste vara gynnsamma för att matcha spool-kapabla regler, och det lokala sammanhanget måste producera ett tillräckligt högt löftesvärde för att optimeraren väljer att generera substitut med hjälp av regeln .

Spoolregler

Det finns ett antal regler som utforskar logiska kapslade loopar eller ansök alternativ. Vissa av dessa regler kan producera ett eller flera substitut med en viss typ av prestationsspole. Andra regler som matchar kapslade loopar ansluter eller tillämpas genererar aldrig ett spoolalternativ.

Till exempel regeln ApplyToNL implementerar en logisk apply som en fysisk loop förenas med yttre referenser. Den här regeln kan generera flera alternativ varje gång den körs. Förutom den fysiska anslutningsoperatören kan varje ersättare innehålla en lazy table spole, en lazy index spole eller ingen spole alls. De logiska spoolersättningarna implementeras senare individuellt och kostnadsberäknas som de lämpligt typade fysiska spolarna, av en annan regel som kallas BuildSpool .

Som ett andra exempel, regeln JNtoIdxLookup implementerar en logisk koppling som en fysisk apply , med en indexsökning omedelbart på insidan. Denna regel aldrig genererar ett alternativ med en spolkomponent. JNtoIdxLookup utvärderas tidigt och returnerar ett högt löftesvärde när det matchar, så enkla indexuppslagsplaner hittas snabbt.

När optimeraren hittar ett billigt alternativ som detta tidigt, kan mer komplexa alternativ beskäras aggressivt eller hoppa över helt. Resonemanget är att det inte är meningsfullt att utöva alternativ som sannolikt inte kommer att förbättras på ett lågkostnadsalternativ som redan finns. På samma sätt är det inte värt att undersöka ytterligare om den nuvarande bästa kompletta planen redan har en tillräckligt låg totalkostnad.

Ett tredje regelexempel:regeln JNtoNL liknar ApplyToNL , men den implementerar bara fysisk kapslad loop-koppling , med antingen en lat bordsspole eller ingen spole alls. Denna regel aldrig genererar en indexspool eftersom den typen av spool kräver en applicering.

Spoolgenerering och kostnadsberäkning

En regel som är kapabel att generera en logisk spool kommer inte nödvändigtvis att göra det varje gång det anropas. Det skulle vara slösaktigt att skapa logiska alternativ som nästan inte har någon chans att bli utvalda som billigast. Det finns också en kostnad för att generera nya alternativ, som i sin tur kan producera ännu fler alternativ – som var och en kan behöva implementeras och kostnadsföras.

För att hantera detta implementerar optimeraren gemensam logik för alla spool-kapabla regler för att bestämma vilken eller vilka typer av spoolalternativ som ska genereras baserat på lokala planvillkor.

Nested loops Join

För en kapslade loopar gå med , chansen att få en lat bordsspole ökar i takt med:

Det uppskattade antalet rader på den yttre ingången av join.
Den uppskattade kostnaden av planoperatörer på insidan.

Kostnaden för spolen återbetalas genom besparingar som görs för att undvika avrättningar på insidan av operatören. Besparingarna ökar med fler inre iterationer och högre kostnader på insidan. Detta gäller särskilt eftersom kostnadsmodellen tilldelar relativt låga I/O- och CPU-kostnadsnummer till bordsspolar (cacheträffar). Kom ihåg att en tabellspole på en kapslad loop-förening bara alltid upplever tillbakaspolning, eftersom avsaknaden av parametrar innebär att insidans datauppsättning är statisk.

En spool kan lagra data tätare än operatörerna som matar den. Till exempel kan ett klustrat index för bastabell lagra 100 rader per sida i genomsnitt. Säg att en fråga bara behöver ett heltalskolumnvärde från varje bred klustrad indexrad. Att bara lagra heltalsvärdet i spoolarbetstabellen innebär att långt över 800 sådana rader kan lagras per sida. Detta är viktigt eftersom optimeraren bedömer kostnaden för bordsspolen delvis med hjälp av en uppskattning av antalet arbetsbordssidor behövs. Andra kostnadsfaktorer inkluderar CPU-kostnaden per rad för att skriva och läsa spoolen, över det uppskattade antalet loop-iterationer.

Optimizern är utan tvekan lite för angelägen om att lägga till lata bordsspolar på insidan av en kapslad ögla. Ändå är optimerarens beslut alltid vettigt i termer av uppskattad kostnad. Jag anser personligen att kapslade loopar går med som hög risk , eftersom de snabbt kan bli långsamma om endera anslutningsindatauppskattningen är för låg.

En bordsspole kan hjälpa till att minska kostnaderna, men det kan inte helt dölja prestandan i värsta fall för en naiv kapslad loop-join. En indexerad appliceringskoppling är normalt att föredra och mer motståndskraftig mot uppskattningsfel. Det är också en bra idé att skriva frågor som optimeraren kan implementera med hash eller merge join när det är lämpligt.

Använd Lazy Table Spool

För en ansökan , chanserna att få en lat bordsspole öka med det uppskattade antalet dubbletter slå samman nyckelvärden på den yttre ingången av appliceringen. Med fler dubbletter finns det en statistiskt större chans att spolen spolar tillbaka sina för närvarande lagrade resultat vid varje iteration. En applicera lat bordsspole med en lägre uppskattad kostnad har en bättre chans att ingå i den slutliga utförandeplanen.

När raderna som kommer till den applicerande yttre ingången inte har någon speciell ordning, gör optimeraren en statistisk bedömning av hur sannolikt varje iteration är att resultera i en billig återspolning eller en dyr ombindning. Den här bedömningen använder data från histogramsteg när de är tillgängliga, men även detta bästa scenario är mer av en välgrundad gissning. Utan garanti är ordningen på raderna som kommer på den applicerade yttre ingången oförutsägbar.

Samma optimeringsregler som genererar logiska spoolalternativ kan också ange att appliceringsoperatorn kräver sorterade rader på dess yttre ingång. Detta maximerar lata spole bakåt eftersom alla dubbletter garanterat påträffas i ett block. När den yttre sorteringsordningen är garanterad, antingen genom bevarad ordning eller en explicit Sortering , är kostnaden för spolen mycket reducerad. Optimizern tar hänsyn till sorteringsordningens inverkan på antalet spolar tillbaka och ombindningar.

Planer med en Sortering på den applicerande yttre ingången och en Lazy Table Spool på den inre ingången är ganska vanliga. Optimeringen av den yttre sorteringen kan ändå bli kontraproduktiv. Detta kan till exempel hända när uppskattningen av den yttre sidans kardinalitet är så låg att sorteringen hamnar i tempdb .

Använd Lazy Index Spool

För en ansökan , får en lat indexspole alternativ beror på planens form såväl som kostnad.

Optimeraren kräver:

Några dubbletter slå samman värden på den yttre ingången.
En jämlikhet join-predikat (eller en logisk motsvarighet som optimeraren förstår, såsom x <= y AND x >= y ).
En garanti att de yttre referenserna är unika under den föreslagna lata indexspolen.

I exekveringsplaner tillhandahålls den erforderliga unikheten ofta av en aggregatgruppering av de yttre referenserna, eller ett skalärt aggregat (en utan grupp efter). Unikhet kan också tillhandahållas på andra sätt, till exempel genom att det finns ett unikt index eller en begränsning.

Ett leksaksexempel som visar planformen är nedan:

CREATE TABLE #T1 
(
    c1 integer NOT NULL
);
GO
INSERT #T1 (c1)
VALUES
    -- Duplicate outer rows
    (1), (2), (3), (4), (5), (6),
    (1), (2), (3), (4), (5), (6),
    (1), (2), (3), (4), (5), (6);
GO
SELECT * 
FROM #T1 AS T1
CROSS APPLY 
(
    SELECT COUNT_BIG(*) 
    FROM (SELECT T1.c1 UNION SELECT NULL) AS U
) AS CA (c);

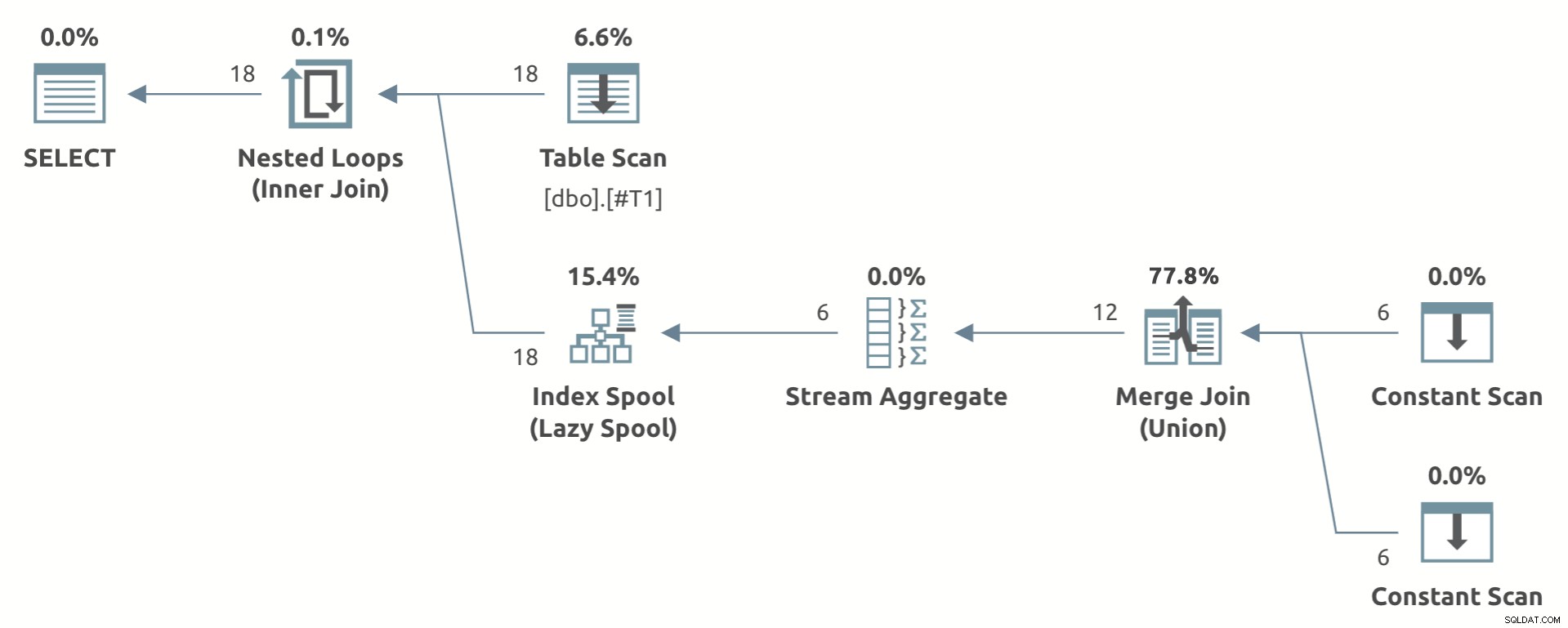
Lägg märke till Strömaggregatet under Lazy Index Spool .

Om kraven på planformen är uppfyllda kommer optimeraren ofta att generera ett lata indexalternativ (med förbehåll för de varningar som nämnts tidigare). Huruvida den slutliga planen innehåller en lat indexspole eller inte beror på kostnaden.

Indexspool kontra bordspool

Antalet beräknade bakåtspolningar och binder om för en lat indexspole är samma som för en lat bordsspole utan sorterade tillämpa yttre inmatning.

Detta kan tyckas vara ett ganska olyckligt tillstånd. Den främsta fördelen med en indexspool är att den cachar alla tidigare sett resultat. Detta borde göra att indexspoolen spolas tillbaka mer sannolikt än för en bordsspole (utan sortering av yttre input) under samma omständigheter. Jag förstår att denna egenhet existerar för utan den skulle optimeraren välja en indexspole alldeles för ofta.

Oavsett vilket justerar kostnadsmodellen för ovanstående till viss del genom att använda olika initiala och efterföljande rad I/O- och CPU-kostnadsnummer för index- och tabellspolar. Nettoeffekten är att en indexspole vanligtvis kostar lägre än en bordsspole utan sorterad yttre ingång, men kom ihåg de restriktiva kraven på planformen, som gör lata indexspolar relativt sällsynt.

Ändå är den primära kostnadskonkurrenten till ett lazy spool-index en bordsspole med sorterad yttre ingång. Intuitionen för detta är ganska okomplicerad:Sorterad yttre input betyder att bordsspolen garanterat ser alla dubbletter av yttre referenser sekventiellt. Det betyder att den kommer att binda om endast en gång per distinkt värde och spola tillbaka för alla dubbletter. Detta är detsamma som det förväntade beteendet för en indexspool (åtminstone logiskt sett).

I praktiken är det mer sannolikt att en indexspool föredras framför en sorteringsoptimerad tabellspool för färre dubbletter av appliceringsnyckelvärden. Att ha färre dubbletter av nycklar minskar spolningen bakåt fördelen med den sorteringsoptimerade tabellspolen, jämfört med de "olyckliga" indexspooluppskattningarna som noterats tidigare.

Alternativet indexspole gynnas också som den uppskattade kostnaden för en bordsspole på utsidan Sortera ökar. Detta skulle oftast vara associerat med fler (eller bredare) rader vid den punkten i planen.

Spåra flaggor och tips

Prestandaspolar kan inaktiveras med lätt dokumenterad spårflagga 8690 , eller det dokumenterade frågetipset NO_PERFORMANCE_SPOOL på SQL Server 2016 eller senare.
Odokumenterad spårningsflagga 8691 kan användas (på ett testsystem) för att alltid lägga till en prestationsspool när det är möjligt. typen av lat spole du får (radantal, tabell eller index) kan inte tvingas fram; det beror fortfarande på kostnadsuppskattning.
Odokumenterad spårningsflagga 2363 kan användas med den nya kardinalitetsuppskattningsmodellen för att se härledningen av den distinkta skattningen på den yttre ingången till en applicera, och kardinalitetsuppskattning i allmänhet.
Odokumenterad spårningsflagga 9198 kan användas för att inaktivera lata indexprestandaspolar specifikt. Du kan fortfarande få en lat tabell eller radräkningsspole istället (med eller utan sorteringsoptimering), beroende på kostnad.
Odokumenterad spårningsflagga 2387 kan användas för att minska CPU-kostnaden av att läsa rader från en lat indexspole . Den här flaggan påverkar generella CPU-kostnadsuppskattningar för att läsa ett antal rader från ett b-träd. Denna flagga tenderar att göra val av indexspool mer sannolikt av kostnadsskäl.

Andra spårningsflaggor och metoder för att avgöra vilka optimeringsregler som aktiverades under frågekompileringen finns i min Query Optimizer Deep Dive-serie.

Slutliga tankar

Det finns väldigt många interna detaljer som påverkar om den slutliga genomförandeplanen använder en prestationsspool eller inte. Jag har försökt täcka de viktigaste övervägandena i den här artikeln, utan att gå för långt in på de extremt intrikata detaljerna i spooloperatörens kostnadsformler. Förhoppningsvis finns det tillräckligt med allmänna råd här för att hjälpa dig att avgöra möjliga orsaker till en viss typ av prestationsspool i en exekveringsplan (eller brist på sådan).

Prestationsspolar får ofta dålig rap tycker jag är rättvist att säga. En del av detta är utan tvekan förtjänt. Många av er kommer att ha sett en demo där en plan körs snabbare utan en "prestationsspole" än med. Till viss del är det inte oväntat. Kantfall finns, kostnadsmodellen är inte perfekt, och utan tvekan innehåller demos ofta planer med dåliga uppskattningar av kardinalitet eller andra problem som begränsar optimeraren.

Som sagt, jag önskar ibland att SQL Server skulle ge någon form av varning eller annan feedback när den tillgriper att lägga till en lazy table spool till en kapslad loop-join (eller en applicering utan ett använt stödjande innersideindex). Som nämnts i huvudtexten är det de här situationerna som jag oftast tycker går snett, när uppskattningar av kardinalitet visar sig vara fruktansvärt låga.

Kanske kommer frågeoptimeraren en dag att ta hänsyn till något riskbegrepp för att planera val, eller tillhandahålla mer "anpassningsbara" möjligheter. Under tiden lönar det sig att stödja dina kapslade loopar med användbara index, och att undvika att skriva frågor som endast kan implementeras med kapslade loopar där det är möjligt. Jag generaliserar förstås, men optimeraren tenderar att bli bättre när den har fler valmöjligheter, ett rimligt schema, bra metadata och hanterbara T-SQL-satser att arbeta med. Liksom jag kommer att tänka på det.

Andra spoolartiklar

Icke-presterande spooler används för många ändamål inom SQL Server, inklusive:

Halloween-skydd
Vissa radlägesfönsterfunktioner
Beräkning av flera aggregat
Optimera uttalanden som ändrar data