Returnerande kombinationer
Använd en taltabell eller nummergenererande CTE, välj 0 till 2^n - 1. Använd bitpositionerna som innehåller 1:or i dessa siffror för att indikera närvaron eller frånvaron av de relativa medlemmarna i kombinationen, och eliminera de som inte har korrekt antal värden, bör du kunna returnera en resultatuppsättning med alla kombinationer du önskar.
WITH Nums (Num) AS (
SELECT Num
FROM Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
), Combos AS (
SELECT
ComboID = N.Num,
S.Value,
Cnt = Count(*) OVER (PARTITION BY N.Num)
FROM
Nums N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
ComboID,
Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;
Den här frågan fungerar ganska bra, men jag tänkte på ett sätt att optimera den, genom att hämta från Snyggt antal parallella bitar för att först få rätt antal föremål tagna åt gången. Detta fungerar 3 till 3,5 gånger snabbare (både CPU och tid):
WITH Nums AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM dbo.Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
FROM Nums2
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
)
SELECT
ComboID = N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;
Jag gick och läste biträkningssidan och tänkte att detta skulle kunna prestera bättre om jag inte gör % 255 utan går hela vägen med bitarithmetik. När jag får en chans ska jag prova det och se hur det går.
Mina prestationsanspråk är baserade på de frågor som körs utan ORDER BY-klausulen. För tydlighetens skull, vad den här koden gör är att räkna antalet set 1-bitar i Num från Numbers tabell. Det beror på att numret används som en sorts indexerare för att välja vilka element i uppsättningen som finns i den aktuella kombinationen, så antalet 1-bitar blir detsamma.
Jag hoppas att du gillar det!
För ordens skull, den här tekniken att använda bitmönstret av heltal för att välja medlemmar i en uppsättning är vad jag har myntat "Vertical Cross Join". Det resulterar effektivt i korskoppling av flera uppsättningar data, där antalet uppsättningar och korskopplingar är godtyckligt. Här är antalet set antalet föremål som tas åt gången.
I själva verket skulle korskoppling i vanlig horisontell bemärkelse (att lägga till fler kolumner till den befintliga listan med kolumner med varje koppling) se ut ungefär så här:
SELECT
A.Value,
B.Value,
C.Value
FROM
@Set A
CROSS JOIN @Set B
CROSS JOIN @Set C
WHERE
A.Value = 'A'
AND B.Value = 'B'
AND C.Value = 'C'
Mina frågor ovan "cross join" effektivt så många gånger som behövs med bara en join. Resultaten är opivoterade jämfört med faktiska korsfogningar, visst, men det är en mindre fråga.
Kritik av din kod
Först vill jag föreslå den här ändringen till din faktoriella UDF:
ALTER FUNCTION dbo.Factorial (
@x bigint
)
RETURNS bigint
AS
BEGIN
IF @x <= 1 RETURN 1
RETURN @x * dbo.Factorial(@x - 1)
END
Nu kan du beräkna mycket större uppsättningar av kombinationer, plus att det är mer effektivt. Du kan till och med överväga att använda decimal(38, 0) för att tillåta större mellanberäkningar i dina kombinationsberäkningar.
För det andra ger din givna fråga inte de korrekta resultaten. Till exempel, med hjälp av mina testdata från prestandatestningen nedan, är set 1 samma som set 18. Det ser ut som att din fråga tar en glidande remsa som sveper sig runt:varje uppsättning är alltid 5 angränsande medlemmar som ser ut ungefär så här (jag svängde för att göra det lättare att se):
1 ABCDE
2 ABCD Q
3 ABC PQ
4 AB OPQ
5 A NOPQ
6 MNOPQ
7 LMNOP
8 KLMNO
9 JKLMN
10 IJKLM
11 HIJKL
12 GHIJK
13 FGHIJ
14 EFGHI
15 DEFGH
16 CDEFG
17 BCDEF
18 ABCDE
19 ABCD Q
Jämför mönstret från mina frågor:
31 ABCDE
47 ABCD F
55 ABC EF
59 AB DEF
61 A CDEF
62 BCDEF
79 ABCD G
87 ABC E G
91 AB DE G
93 A CDE G
94 BCDE G
103 ABC FG
107 AB D FG
109 A CD FG
110 BCD FG
115 AB EFG
117 A C EFG
118 BC EFG
121 A DEFG
...
Bara för att köra bitmönstret -> index för kombinationssaken hem för alla som är intresserade, lägg märke till att 31 i binär =11111 och mönstret är ABCDE. 121 i binär är 1111001 och mönstret är A__DEFG (bakåt mappat).
Prestanda resultat med en tabell med reella siffror
Jag körde en del prestandatester med stora uppsättningar på min andra fråga ovan. Jag har för närvarande ingen uppgift om serverversionen som används. Här är mina testdata:
DECLARE
@k int,
@n int;
DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;
DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);
Peter visade att denna "vertical cross join" inte fungerar lika bra som att bara skriva dynamisk SQL för att faktiskt göra de CROSS JOINs den undviker. Till den triviala kostnaden av några fler läsningar har hans lösning mätvärden mellan 10 och 17 gånger bättre. Prestandan för hans sökfråga minskar snabbare än min när mängden arbete ökar, men inte tillräckligt snabbt för att hindra någon från att använda den.
Den andra uppsättningen siffror nedan är faktorn dividerad med den första raden i tabellen, bara för att visa hur den skalas.
Erik
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 7344 0 3861 8531 |
18•9 17141 0 7748 18536 | 2.3 2.0 2.2
20•10 76657 0 34078 84614 | 10.4 8.8 9.9
21•11 163859 0 73426 176969 | 22.3 19.0 20.7
21•20 142172 0 71198 154441 | 19.4 18.4 18.1
Peter
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 422 70 10263 794 |
18•9 6046 980 219180 11148 | 14.3 14.0 21.4 14.0
20•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.1
21•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.3
21•20 51391 5 6291273 55169 | 121.8 0.1 613.0 69.5
Extrapolerar, så kommer min fråga så småningom att bli billigare (även om det är från början i läsningar), men inte på länge. För att använda 21 objekt i uppsättningen krävs redan en siffertabell som går upp till 2097152...
Här är en kommentar som jag ursprungligen gjorde innan jag insåg att min lösning skulle prestera drastiskt bättre med en siffertabell i farten:
Prestanda resultat med en On-The-Fly siffror tabell
När jag ursprungligen skrev det här svaret sa jag:
Tja, jag provade det, och resultatet var att det fungerade mycket bättre! Här är frågan jag använde:
DECLARE @N int = 16, @K int = 12;
CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set
SELECT TOP (@N) V
FROM
(VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
@N int = (SELECT Count(*) FROM #Set),
@K int = (SELECT TOP 1 Num FROM #Items);
DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM Nums
WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums1
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
FROM Nums2
), BaseSet AS (
SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM #Set
)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;
Observera att jag valde värdena i variabler för att minska tiden och minnet som behövs för att testa allt. Servern gör fortfarande samma arbete. Jag modifierade Peters version för att vara liknande, och tog bort onödiga extrafunktioner så att de båda var så magra som möjligt. Serverversionen som används för dessa tester är Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) körs på en virtuell dator.
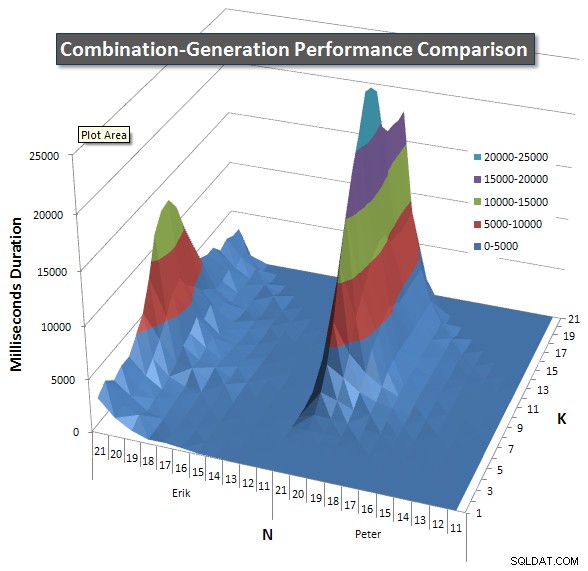
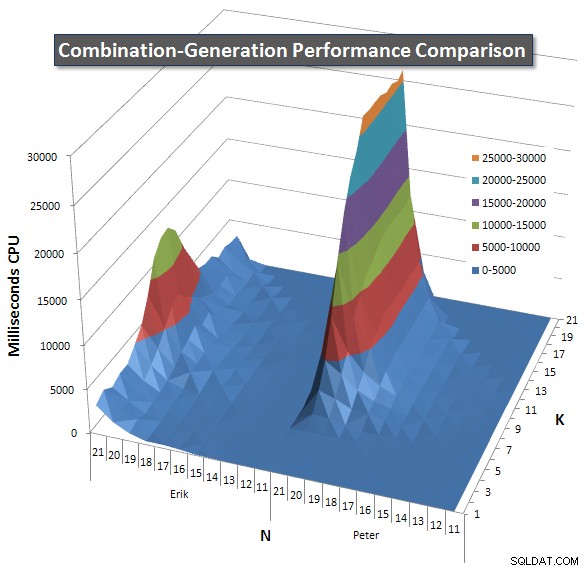
Nedan visas diagram som visar prestandakurvorna för värden på N och K upp till 21. Basdata för dem finns i ett annat svar på den här sidan . Värdena är resultatet av 5 körningar av varje fråga vid varje K- och N-värde, följt av att de bästa och sämsta värdena för varje mätvärde tas ut och genomsnittet av de återstående 3.
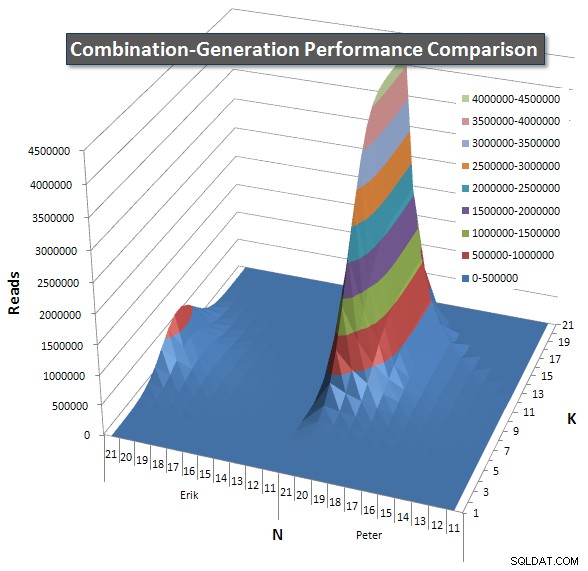
I grund och botten har min version en "axel" (i det vänstra hörnet av diagrammet) vid höga värden på N och låga värden på K som gör att den presterar sämre där än den dynamiska SQL-versionen. Detta förblir dock ganska lågt och konstant, och den centrala toppen runt N =21 och K =11 är mycket lägre för Duration, CPU och Reads än den dynamiska SQL-versionen.
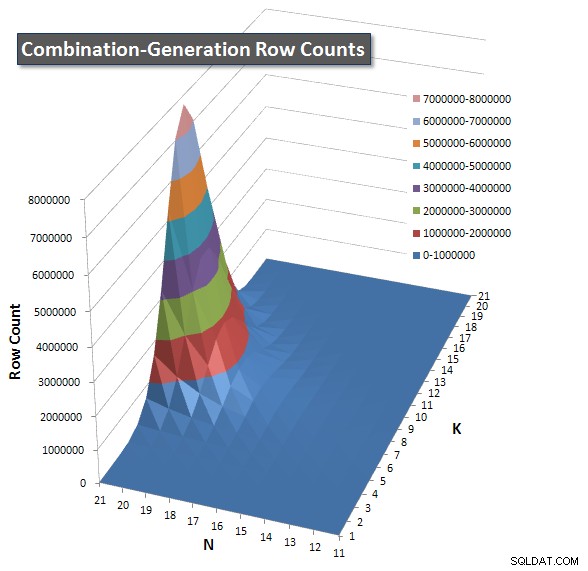
Jag inkluderade ett diagram över antalet rader varje objekt förväntas returnera så att du kan se hur frågan presterar i förhållande till hur stort jobb den måste göra.
Se mitt ytterligare svar på den här sidan för de fullständiga prestationsresultaten. Jag nådde gränsen för posttecken och kunde inte inkludera den här. (Några idéer om var man kan lägga det annars?) För att sätta saker i perspektiv mot min första versions prestandaresultat, här är samma format som tidigare:
Erik
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 354 378 12382 0 |
18•9 1849 1893 97246 0 | 5.2 5.0 7.9
20•10 7119 7357 369518 0 | 20.1 19.5 29.8
21•11 13531 13807 705438 0 | 38.2 36.5 57.0
21•20 3234 3295 48 0 | 9.1 8.7 0.0
Peter
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 41 45 6433 0 |
18•9 2051 1522 214021 0 | 50.0 33.8 33.3
20•10 8271 6685 864455 0 | 201.7 148.6 134.4
21•11 18823 15502 2097909 0 | 459.1 344.5 326.1
21•20 25688 17653 4195863 0 | 626.5 392.3 652.2
Slutsatser
- On-the-fly siffertabeller är bättre än en riktig tabell som innehåller rader, eftersom att läsa en med enorma radantal kräver mycket I/O. Det är bättre att använda lite CPU.
- Mina initiala tester var inte tillräckligt breda för att verkligen visa prestandaegenskaperna hos de två versionerna.
- Peters version kan förbättras genom att göra att varje JOIN inte bara är större än det föregående objektet, utan också begränsa maxvärdet baserat på hur många fler objekt som måste passa in i setet. Till exempel, vid 21 objekt tagna 21 åt gången, finns det bara ett svar på 21 rader (alla 21 objekt, en gång), men de mellanliggande raduppsättningarna i den dynamiska SQL-versionen, tidigt i exekveringsplanen, innehåller kombinationer som " AU" i steg 2 även om detta kommer att kasseras vid nästa koppling eftersom det inte finns något värde högre än "U" tillgängligt. På liknande sätt kommer en mellanraduppsättning i steg 5 att innehålla "ARSTU", men den enda giltiga kombinationen vid denna tidpunkt är "ABCDE". Denna förbättrade version skulle inte ha en lägre topp i mitten, så kanske inte förbättra den tillräckligt för att bli den klara vinnaren, men den skulle åtminstone bli symmetrisk så att sjökorten inte skulle hålla sig maxade förbi mitten av regionen utan skulle falla tillbaka till nära 0 som min version gör (se det övre hörnet av topparna för varje fråga).
Varaktighetsanalys
- Det finns ingen riktigt signifikant skillnad mellan versionerna i varaktighet (>100ms) förrän 14 objekt tagna 12 åt gången. Fram till denna punkt vinner min version 30 gånger och den dynamiska SQL-versionen vinner 43 gånger.
- Från 14•12 var min version snabbare 65 gånger (59>100ms), den dynamiska SQL-versionen 64 gånger (60>100ms). Men alla gånger min version var snabbare sparade den en total genomsnittlig varaktighet på 256,5 sekunder, och när den dynamiska SQL-versionen var snabbare sparade den 80,2 sekunder.
- Den totala genomsnittliga längden för alla försök var Erik 270,3 sekunder, Peter 446,2 sekunder.
- Om en uppslagstabell skapades för att bestämma vilken version som ska användas (välja den snabbare för ingångarna), kunde alla resultat utföras på 188,7 sekunder. Att använda den långsammaste varje gång skulle ta 527,7 sekunder.
Läsanalys
Varaktighetsanalysen visade att min fråga vann med betydande men inte alltför stora belopp. När måttet växlas till läsningar framträder en helt annan bild - min fråga använder i genomsnitt 1/10 av läsningarna.
- Det finns ingen riktigt signifikant skillnad mellan versionerna i läsningar (>1000) förrän 9 objekt togs 9 åt gången. Fram till denna punkt vinner min version 30 gånger och den dynamiska SQL-versionen vinner 17 gånger.
- Från 9•9 använde min version färre läsningar 118 gånger (113>1000), den dynamiska SQL-versionen 69 gånger (31>1000). Men alla gånger min version använde färre läsningar sparade den i genomsnitt 75,9 miljoner läsningar, och när den dynamiska SQL-versionen var snabbare sparade den 380 000 läsningar.
- Det totala genomsnittliga antalet avläsningar för alla försök var Erik 8,4 miljoner, Peter 84 miljoner.
- Om en uppslagstabell skapades för att bestämma vilken version som ska användas (välja den bästa för ingångarna), kunde alla resultat utföras i 8M läsningar. Att använda den sämsta varje gång skulle ta 84,3 miljoner läsningar.
Jag skulle vara mycket intresserad av att se resultaten av en uppdaterad dynamisk SQL-version som sätter den extra övre gränsen för de objekt som väljs vid varje steg som jag beskrev ovan.
Tillägg
Följande version av min fråga uppnår en förbättring på cirka 2,25 % jämfört med prestandaresultaten som anges ovan. Jag använde MIT:s HAKMEM biträkningsmetod och lade till en Convert(int) på resultatet av row_number() eftersom det ger en bigint. Naturligtvis önskar jag att det här var den version jag hade använt med för alla prestandatester och diagram och data ovan, men det är osannolikt att jag någonsin kommer att göra om det eftersom det var arbetskrävande.
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Convert(int, Num) Num
FROM Nums
WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
SELECT
Num,
P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
Bits = @K
Och jag kunde inte motstå att visa en version till som gör en uppslagning för att få antalet bitar. Det kan till och med vara snabbare än andra versioner:
DECLARE @BitCounts binary(255) =
0x01010201020203010202030203030401020203020303040203030403040405
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums1 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
@K =
Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))
