SQL Server Join Estimation med Histogram Coarse Alignment

De primära ändringarna som gjorts i Cardinality Estimation från och med SQL Server 2014-versionen beskrivs i Microsoft White Paper Optimizing Your Query Plans with SQL Server 2014 Cardinality Estimator av Joe Sack, Yi Fang och Vassilis Papadimos.

En av dessa ändringar gäller uppskattningen av enkla kopplingar med ett enda likhets- eller ojämlikhetspredikat med hjälp av statistikhistogram. I avsnittet med rubriken "Join Estimate Algorithm Changes" introducerade tidningen konceptet "grovjustering" med minimala och maximala histogramgränser:

Även om det är potentiellt mindre konsekvent, kan den äldre CE:n producera något bättre uppskattningar av enkel sammanfogning tillstånd på grund av steg-för-steg-histogramjusteringen. Den nya CE använder en grov linje. Skillnaden i uppskattningar kan dock vara tillräckligt liten för att det är mindre troligt att det orsakar kvalitetsproblem i planen.

Som en av de tekniska granskarna av tidningen kände jag att lite mer detaljer kring denna förändring skulle ha varit användbar, men det kom inte in i den slutliga versionen. Den här artikeln lägger till en del av den detaljen.

Exempel på grovhistogramjustering

grovjusteringen exempel i vitboken använder Data Warehouse-versionen av exempeldatabasen AdventureWorks. Trots namnet är databasen ganska liten; säkerhetskopian är bara 22,3 MB och utökas till cirka 200 MB. Den kan laddas ner via länkar på AdventureWorks installations- och konfigurationsdokumentationssida.

Frågan vi är intresserade av ansluter sig till FactResellerSales och FactCurrencyRate tabeller.

SELECT
    FRS.ProductKey,
    FRS.OrderDateKey,
    FRS.DueDateKey,
    FRS.ShipDateKey,
    FCR.DateKey,
    FCR.AverageRate,
    FCR.EndOfDayRate,
    FCR.[Date]
FROM dbo.FactResellerSales AS FRS
JOIN dbo.FactCurrencyRate AS FCR
    ON FCR.CurrencyKey = FRS.CurrencyKey;

Detta är en enkel equijoin på en enda kolumn så det kvalificerar sig för sammanfogningskardinalitet och selektivitetsuppskattning med histogram grovjustering.

Histogram

Histogrammen vi behöver är associerade med CurrencyKey kolumn på varje sammanfogad tabell. På en ny kopia av AdventureWorksDW-databasen, den redan existerande statistiken för de större FactResellerSales Tabellen baseras på ett prov. För att maximera reproducerbarheten och göra de detaljerade beräkningarna så enkla som möjligt att följa (för att undvika skalning), är det första vi kommer att göra att uppdatera statistiken med en fullständig skanning:

UPDATE STATISTICS dbo.FactCurrencyRate WITH FULLSCAN;
UPDATE STATISTICS dbo.FactResellerSales WITH FULLSCAN;

Dessa tabeller har den demovänliga fördelen att de skapar små och enkla maxdiff histogram:

DBCC SHOW_STATISTICS
    (FactResellerSales, CurrencyKey)
WITH HISTOGRAM;
 
DBCC SHOW_STATISTICS
    (FactCurrencyRate, [PK_FactCurrencyRate_CurrencyKey_DateKey])
WITH HISTOGRAM;

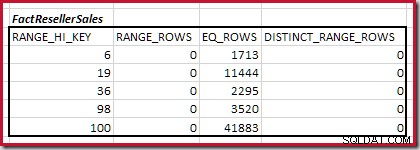
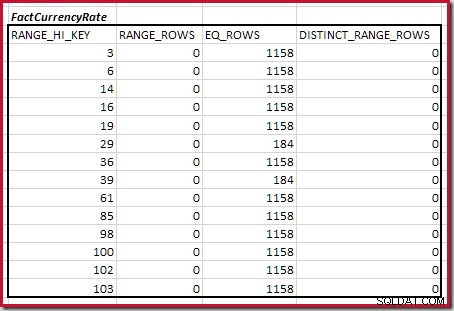
Kombinera minsta matchande histogramsteg

Det första steget i grovjusteringen beräkningen är att hitta bidraget till kopplingskardinaliteten från det lägsta matchande histogramsteget. För våra exempelhistogram är det minsta matchningsstegvärdet på RANGE_HI_KEY = 6 :

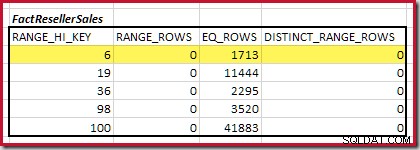
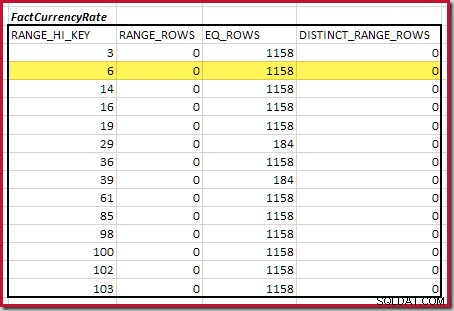
Den uppskattade equijoin-kardinaliteten för bara detta markerade steg är 1 713 * 1 158 =1 983 654 rader .

Återstående matchade steg

Därefter måste vi identifiera området för histogram RANGE_HI_KEY steg upp till det maximala för möjliga equijoin-matcher. Detta innebär att gå framåt från det tidigare hittade minimum tills en av histogramingångarna tar slut på rader. De matchande equijoin-intervallen för det aktuella exemplet är markerade nedan:

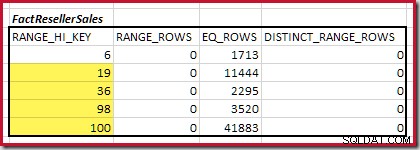
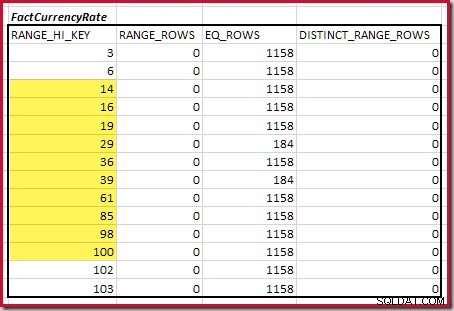
Dessa två intervall representerar de återstående raderna som kan förväntas bidra till equijoin-kardinalitet.

Grovfrekvensbaserad uppskattning

Frågan är nu hur man utför ett grovt uppskattning av equijoin-kardinaliteten för de markerade stegen, med hjälp av tillgänglig information.

Den ursprungliga kardinalitetsuppskattaren skulle ha utfört en finkornig steg-för-steg-histogramjustering med linjär interpolation, bedömt sammanfogningsbidraget för varje steg (ungefär som vi gjorde för det lägsta stegvärdet tidigare) och summerat varje stegbidrag för att få en fullständig uppskattning av sammanfogningen. Även om det här förfarandet är mycket intuitivt vettigt, var praktiska erfarenheter att detta finkorniga tillvägagångssätt ökade beräkningskostnader och kunde ge resultat av varierande kvalitet.

Den ursprungliga skattaren hade ett annat sätt att uppskatta sammanfogningskardinalitet när histograminformation antingen inte var tillgänglig eller heuristiskt bedömdes vara sämre. Detta är känt som en frekvensbaserad uppskattning och använder följande definitioner:

• C – kardinalitet (antal rader)
• D – antalet distinkta värden
• F – frekvensen (antal rader) för varje distinkt värde
• Obs C =D * F per definition

Effekten av en ekvijoin av relationerna R1 och R2 på var och en av dessa egenskaper är som visas nedan:

• F' =F1 * F2
• D' =MIN(D1; D2) – förutsatt inneslutning
• C' =D' * F' (igen, per definition)

Vi är efter C', ekvijoinens kardinalitet. Ersätter D' och F' i formeln och expanderar:

• C' =D' * F'
• C' =MIN(D1; D2) * F1 * F2
• C' =MIN(D1 * F1 * F2; D2 * F1 * F2)
• nu, eftersom C1 =D1 * F1 och C2 =D2 * F2:
• C' =MIN(C1 * F2, C2 * F1)
• slutligen, eftersom F =C/D (även per definition):
• C' =MIN(C1 * C2 / D2; C2 * C1 / D1)

När man noterar att C1 * C2 är produkten av de två indatakardinaliteterna (kartesisk sammanfogning), är det tydligt att minimum av dessa uttryck kommer att vara det med det högre antalet distinkta värden:

• C' =(C1 * C2) / MAX(D1; D2)

Om allt detta verkar lite abstrakt, är ett intuitivt sätt att tänka på frekvensbaserad ekvijoin-uppskattning att överväga att varje distinkt värde från en relation kommer att förenas med ett antal rader (medelfrekvensen) i den andra relationen. Om vi ​​har 5 distinkta värden på ena sidan, och varje distinkt värde på den andra sidan visas 3 gånger i genomsnitt, är en förnuftig (men grov) equijoin-uppskattning 5 * 3 =15.

Det här är inte riktigt en så bred borste som det kan verka. Kom ihåg att siffrorna för kardinalitet och distinkta värden ovan inte kommer från hela relationen, utan bara från matchningsstegen över minimum. Därav grov uppskattning mellan minimi- och maximivärden.

Frekvensberäkning

Vi kan få var och en av dessa parametrar från de markerade histogramstegen.

• Kardinaliteten C är summan av EQ_ROWS och RANGE_ROWS .
• Antalet distinkta värden D är summan av DISTINCT_RANGE_ROWS plus en för varje steg.

Kardinalitet C1 för matchande FactResellerSales steg är summan av de markerade cellerna:

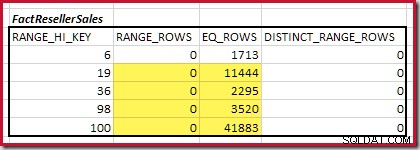
Detta ger C1 =59 142 rader.

Det finns inga distinkta intervallrader, så de enda distinkta värdena kommer från själva fyra stegsgränserna, vilket ger D1 =4 .

För det andra bordet:

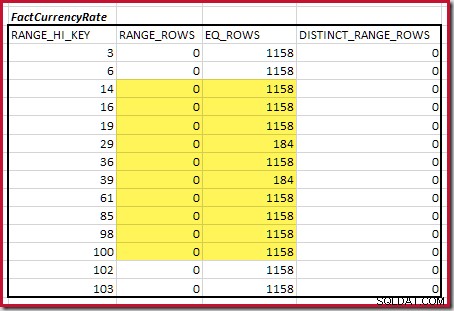
Detta ger C2 =9 632 . Återigen finns det inga distinkta intervallrader, så de distinkta värdena kommer från de tio stegs gränserna, D2 =10.

Slutföra Equijoin-uppskattningen

Vi har nu alla siffror vi behöver för equijoin-formeln:

• C' =(C1 * C2) / MAX(D1; D2)
• C' =(59142 * 9632) / MAX(4; 10)
• C' =569655744 / 10
• C' =56 965 574,4

Kom ihåg att detta är bidraget från histogramstegen över den minsta matchade gränsen. För att slutföra uppskattningen av anslutningskardinalitet måste vi lägga till bidraget från de minsta matchningsstegvärdena, som var 1 713 * 1 158 =1 983 654 rader.

Den slutliga equijoin-uppskattningen är därför 56 965 574,4 + 1 983 654 =58 949 228,4 rader eller 58 949 200 till sex betydande siffror.

Detta resultat bekräftas i den beräknade exekveringsplanen för källfrågan:

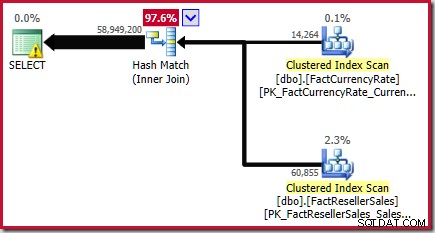
Som noterats i vitboken är detta ingen stor uppskattning. Det faktiska antalet rader som returneras av den här frågan är 70 470 090 . Uppskattningen som produceras av den ursprungliga ("legacy") kardinalitetsuppskattaren – med hjälp av steg-för-steg histogramjustering – är 70 470 100 rader.

Bättre resultat är ofta möjligt med den finare metoden, men bara om statistiken är en mycket bra representation av den underliggande datafördelningen. Detta är inte bara en fråga om att hålla statistiken uppdaterad, eller att använda full scan population. Algoritmen som används för att packa information i maximalt 201 histogramsteg är inte perfekt, och i alla fall är många verkliga datadistributioner helt enkelt inte kapabla till sådan histogramtrohet. I genomsnitt borde människor upptäcka att den grövre metoden ger helt adekvata uppskattningar och större stabilitet med den nya CE.

Andra exemplet

Detta bygger lite på det tidigare exemplet och kräver ingen nedladdning av exempeldatabas.

DROP TABLE IF EXISTS
    dbo.R1,
    dbo.R2;
 
CREATE TABLE dbo.R1 (n integer NOT NULL);
CREATE TABLE dbo.R2 (n integer NOT NULL);
 
INSERT dbo.R1
    (n)
VALUES
    (1), (2), (3), (4), (5), (6), (7), (8), (9), (10),
    (6), (6), (6), (6), (6), (6), (6), (6), (6), (6), 
    (6), (6), (6), (6), (6), (6), (6), (6), (6);
 
INSERT dbo.R2
    (n)
VALUES
    (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15),
    (10), (10);
 
CREATE STATISTICS stats_n ON dbo.R1 (n) WITH FULLSCAN;
CREATE STATISTICS stats_n ON dbo.R2 (n) WITH FULLSCAN;

Histogrammen som visar matchade minimisteg är:

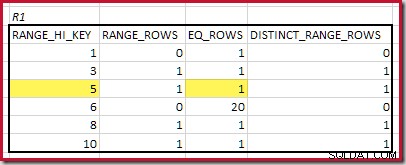
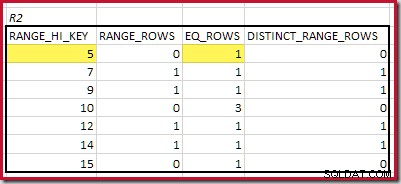
Den lägsta RANGE_HI_KEY som matchar är 5. Värdet på EQ_ROWS är 1 i båda, så den beräknade ekvijoin-kardinaliteten är 1 * 1 =1 rad .

Den högsta matchande RANGE_HI_KEY är 10. Markera R1-histogramraderna för grov frekvensbaserad uppskattning:

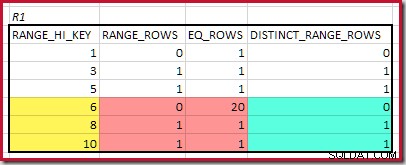
Summera EQ_ROWS och RANGE_ROWS ger C1 =24 . Antalet distinkta rader är 2 DISTINCT_RANGE_ROWS (distinkta värden mellan steg) plus 3 för de distinkta värdena som är associerade med varje steggräns, vilket ger D1 =5 .

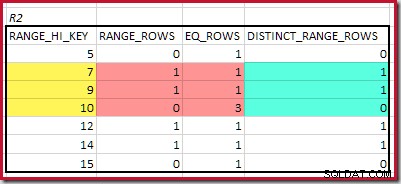
För R2, summera EQ_ROWS och RANGE_ROWS ger C2 =7 . Antalet distinkta rader är 2 DISTINCT_RANGE_ROWS (distinkta värden mellan steg) plus 3 för de distinkta värdena som är associerade med varje steggräns, vilket ger D2 =5 .

Equijoin-uppskattningen C' är:

• C' =(C1 * C2) / MAX(D1; D2)
• C' =(24 * 7) / 5
• C' =33.6

Lägger till i 1 rad från minimistegsmatchningen ger en total uppskattning på 34,6 rader för equijoin:

SELECT
    R1.n,
    R2.n
FROM dbo.R1 AS R1
JOIN dbo.R2 AS R2
    ON R2.n = R1.n;

Den beräknade utförandeplanen visar en uppskattning som matchar vår beräkning:

Detta är inte helt rätt, men den "legacy" kardinalitetsuppskattaren gör inget bättre, den uppskattar 15,25 rader mot 27 faktiska:

För en fullständig behandling skulle vi också behöva lägga till ett sista bidrag från matchande histogram noll-steg, men detta är ovanligt för equijoins (som vanligtvis skrivs för att avvisa nollor) och en relativt enkel förlängning för den intresserade läsaren.

Sluta tankar

Förhoppningsvis kommer detaljerna i artikeln att fylla i några luckor för alla som någonsin undrat över "grov justering". Observera att detta bara är en liten komponent i kardinalitetsuppskattaren. Det finns flera andra viktiga koncept och algoritmer som används för uppskattning av sammanfogningar, särskilt hur icke-sammanfogade predikat bedöms och hur mer komplexa sammanfogningar hanteras. Många av de riktigt viktiga bitarna är ganska väl täckta i vitboken.