Om du letar efter en approximationsalgoritm föreslår jag att du letar efter en k-medelsalgoritm eller ett hierarkiskt kluster, speciellt en monsterkurva eller en rymdfyllningskurva. Först och främst kan du beräkna ett minimalt spännträd i grafen och sedan ta bort de längsta och dyraste kanterna. Sedan bildar trädet många små träd och du kan använda k-medel för att beräkna grupp av punkter, dvs kluster.
"Enlänks k-klustringsalgoritmen ... är just Kruskals algoritm ... likvärdig med att hitta en MST och ta bort de k-1 dyraste kanterna." Se till exempel här:https://stats.stackexchange.com/ question/1475/visualization-software-for-clustering .
Ett bra exempel på en monsterkurva är hilbertkurvan. Den grundläggande formen av denna kurva är en U-form och genom att kopiera många av den tillsammans och rotera den fyller kurvan det euklidiska rummet. Överraskande nog kan en grå kod hjälpa till att ta reda på orienteringen av denna U-form. Du kan slå upp Nicks rumsliga index quadtree hilbert-kurva bloggartikel om mer information . Istället för att beräkna kurvans index kan du sätta ihop en quadkey som i bing-kartor. Fyrnyckeln är unik för varje koordinat och den kan användas med normala strängoperationer. Varje position i tangenten är en del av den U-formade kurvan och därför kan du välja denna region av punkter från att välja delvis från vänster till höger från fyrtangenten.
I den här bilden kan du se att den gröna polygonen hittas med hjälp av en hilbertkurva:
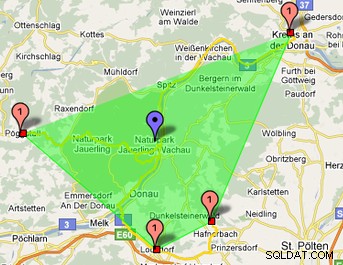
Du kan hitta mina php-klasser här:https://www.phpclasses.org/package/6202-PHP-Generate-points-of-an-Hilbert-curve.html
