Den här artikeln undersöker selektivitets- och kardinalitetsuppskattning för predikat på COUNT(*) uttryck, som kan ses i HAVING klausuler. Detaljerna är förhoppningsvis intressanta i sig. De ger också en inblick i några av de allmänna tillvägagångssätt och algoritmer som används av kardinalitetsskattaren.
Ett enkelt exempel med hjälp av exempeldatabasen AdventureWorks:
SELECT A.City FROM Person.[Address] AS A GROUP BY A.City HAVING COUNT_BIG(*) = 1;
Vi är intresserade av att se hur SQL Server härleder en uppskattning för predikatet på count-uttrycket i HAVING klausul.
Naturligtvis HAVING klausul är bara syntax socker. Vi kunde likaså ha skrivit frågan med en härledd tabell, eller vanligt tabelluttryck:
-- Derived table
SELECT SQ1.City
FROM
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
) AS SQ1
WHERE SQ1.Expr1001 = 1;
-- CTE
WITH Grouped AS
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
)
SELECT G.City
FROM Grouped AS G
WHERE G.Expr1001 = 1; Alla tre frågeformulär producerar samma exekveringsplan, med identiska hashvärden för frågeplan.
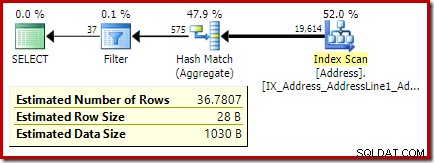
Planen efter genomförandet (faktisk) visar en perfekt uppskattning för aggregatet; dock uppskattningen för HAVING klausulfiltret (eller motsvarande, i de andra frågeformulären) är dåligt:
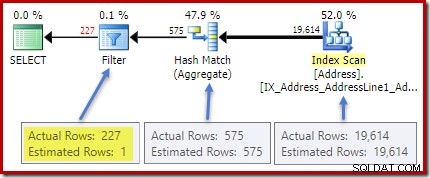
Statistik för City kolumnen ger korrekt information om antalet distinkta stadsvärden:
DBCC SHOW_STATISTICS ([Person.Address], City) WITH DENSITY_VECTOR;
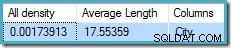
all densitet siffran är det ömsesidiga antalet unika värden. Beräknar helt enkelt (1 / 0,00173913) =575 ger kardinalitetsuppskattningen för aggregatet. Gruppering efter stad ger uppenbarligen en rad för varje distinkt värde.
Observera att all densitet kommer från densitetsvektorn. Var noga med att inte använda densiteten av misstag värde från statistikhuvudets utdata för DBCC SHOW_STATISTICS . Rubrikdensiteten bibehålls endast för bakåtkompatibilitet; den används inte av optimeraren under kardinalitetsuppskattning nu för tiden.
Problemet
Aggregatet introducerar en ny beräknad kolumn i arbetsflödet, märkt Expr1001 i genomförandeplanen. Den innehåller värdet COUNT(*) i varje grupperad utdatarad:
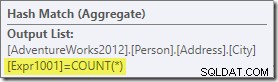
Det finns uppenbarligen ingen statistisk information i databasen om denna nya beräknade kolumn. Även om optimeraren vet att det kommer att finnas 575 rader, vet den ingenting om distributionen av räknevärden inom dessa rader.
Tja, inte riktigt ingenting:Optimeraren är medveten om att räknevärdena kommer att vara positiva heltal (1, 2, 3...). Ändå är det fördelningen av dessa heltalsvärden mellan de 575 raderna som skulle behövas för att exakt uppskatta selektiviteten för COUNT(*) = 1 predikat.
Man skulle kunna tro att någon form av distributionsinformation skulle kunna härledas från histogrammet, men histogrammet ger bara specifik räkningsinformation (i EQ_ROWS ) för histogramstegvärden. Mellan histogramstegen har vi bara en sammanfattning:RANGE_ROWS rader har DISTINCT_RANGE_ROWS distinkta värden. För tabeller som är tillräckligt stora för att vi bryr oss om kvaliteten på selektivitetsuppskattningen är det mycket troligt att större delen av tabellen representeras av dessa sammanfattningar inom steg.
Till exempel, de två första raderna i City kolumnhistogrammen är:
DBCC SHOW_STATISTICS ([Person.Address], City) WITH HISTOGRAM;

Detta säger oss att det finns exakt en rad för "Abingdon" och 29 andra rader efter "Abingdon" men före "Ballard", med 19 distinkta värden i det 29-radsintervallet. Följande fråga visar den faktiska fördelningen av rader mellan unika värden i det intervallet med 29 rader inom steg:
SELECT A.City, NumRows = COUNT_BIG(*) FROM Person.[Address] AS A WHERE A.City > N'Abingdon' AND A.City < N'Ballard' GROUP BY ROLLUP (A.City);

Det finns 29 rader med 19 distinkta värden, precis som histogrammet sa. Ändå är det tydligt att vi inte har någon grund för att utvärdera selektiviteten för ett predikat på räknekolumnen i den frågan. Till exempel, HAVING COUNT_BIG(*) = 2 skulle returnera 5 rader (för Alexandria, Altadena, Atlanta, Augsburg och Austin) men vi har inget sätt att avgöra det från histogrammet.
En utbildad gissning
Tillvägagångssättet för SQL Server är att anta att varje grupp är mest troligt för att innehålla det totala genomsnittliga (genomsnittliga) antalet rader. Detta är helt enkelt kardinaliteten dividerad med antalet unika värden. Till exempel, för 1000 rader med 20 unika värden, skulle SQL Server anta att (1000 / 20) =50 rader per grupp är det mest sannolika värdet.
Om vi vänder tillbaka till vårt ursprungliga exempel betyder detta att kolumnen för beräknat antal "mest troligt" innehåller ett värde runt (19614 / 575) ~=34.1113 . Sedan density är det ömsesidiga antalet unika värden, kan vi också uttrycka det som kardinalitet * densitet =(19614 * 0,00173913), vilket ger ett mycket liknande resultat.
Distribution
Att säga att medelvärdet är mest troligt tar oss bara så långt. Vi måste också fastställa exakt hur troligt det är; och hur sannolikheten förändras när vi går bort från medelvärdet. Att anta att alla grupper har exakt 34.113 rader i vårt exempel skulle inte vara en särskilt "utbildad" gissning!
SQL Server hanterar detta genom att anta en normalfördelning. Denna har den karakteristiska klockformen som du kanske redan känner till (bild från den länkade Wikipedia-posten):
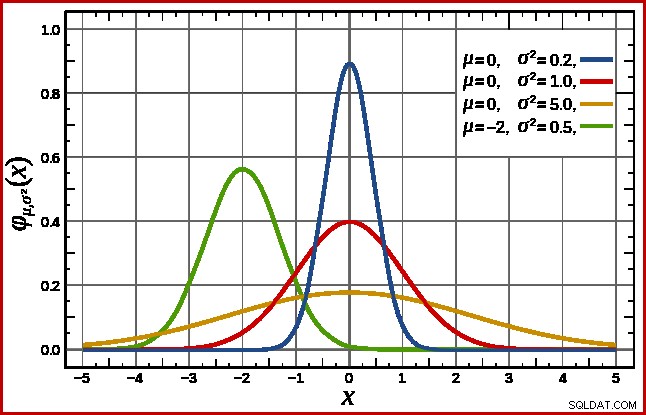
Den exakta formen på normalfördelningen beror på två parametrar :medelvärdet (µ ) och standardavvikelsen (σ ). Medelvärdet bestämmer platsen för toppen. Standardavvikelsen anger hur "tillplattad" klockkurvan är. Ju plattare kurva är, desto lägre är toppen, och desto mer fördelas sannolikhetstätheten över andra värden.
SQL Server kan härleda medelvärdet från statistisk information som redan noterats. Standardavvikelsen av kolumnvärdena för beräknat antal är okända. SQL Server uppskattar det som kvadratroten av medelvärdet (med en liten justering i detalj senare). I vårt exempel betyder det att de två parametrarna för normalfördelningen är ungefär 34,1113 och 5,84 (kvadratroten).
standarden normalfördelning (den röda kurvan i diagrammet ovan) är ett anmärkningsvärt specialfall. Detta inträffar när medelvärdet är noll och standardavvikelsen är 1. Vilken normalfördelning som helst kan omvandlas till standardnormalfördelningen genom att subtrahera medelvärdet och dividera med standardavvikelsen.
Ytor och intervall
Vi är intresserade av att uppskatta selektivitet, så vi letar efter sannolikheten att den räknade kolumnen har ett visst värde (x). Denna sannolikhet ges inte av y-axelns värde ovan, utan av arean under kurvan till vänster om x.
För normalfördelningen med medelvärde 34,1113 och standardavvikelse 5,84 är arean under kurvan till vänster om x =30 cirka 0,2406:
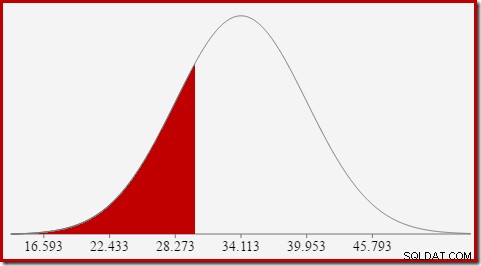
Detta motsvarar sannolikheten att kolumnen för beräknat antal är mindre än eller lika med 30 för vår exempelfråga.
Detta leder bra vidare till idén att vi i allmänhet inte letar efter sannolikheten för ett specifikt värde, utan efter ett intervall . För att hitta sannolikt att antalet lika ett heltalsvärde måste vi ta hänsyn till det faktum att heltal spänner över ett intervall av storlek 1. Hur vi omvandlar ett heltal till ett intervall är något godtyckligt. SQL Server hanterar detta genom att lägga till och subtrahera 0,5 för att ge de nedre och övre gränserna för intervallet.
Till exempel, för att hitta sannolikheten att det beräknade räknevärdet är lika med 30, måste vi subtrahera arean under normalfördelningskurvan för (x =29,5) från arean för (x =30,5). Resultatet motsvarar segmentet för (29,5
Arean av den röda skivan är ungefär 0,0533 . Till en bra första approximation är detta selektiviteten för ett count =30 predikat i vår testfråga.
Att beräkna arean under en normalfördelning till vänster om ett givet värde är inte okomplicerat. Den allmänna formeln ges av den kumulativa fördelningsfunktionen (CDF). Problemet är att CDF inte kan uttryckas i termer av elementära matematiska funktioner, så numeriska approximationsmetoder måste användas istället.
Eftersom alla normalfördelningar lätt kan transformeras till standardnormalfördelningen (medelvärde =0, standardavvikelse =1), fungerar alla approximationer för att uppskatta standardnormalen. Det betyder att vi måste omvandla våra intervallgränser från den specifika normalfördelningen som är lämplig för frågan, till standardnormalfördelningen. Detta görs, som tidigare nämnt, genom att subtrahera medelvärdet och dividera med standardavvikelsen.
Om du är bekant med Excel kanske du känner till funktionerna NORM.DIST och NORM.S.DIST som kan beräkna CDF:er (med numeriska approximationsmetoder) för en viss normalfördelning eller standardnormalfördelningen.
Det finns ingen CDF-kalkylator inbyggd i SQL Server, men vi kan enkelt göra en. Med tanke på att CDF för standardnormalfördelningen är:
…där erf är felfunktionen:
En T-SQL-implementering för att erhålla CDF för normal normalfördelning visas nedan. Den använder en numerisk uppskattning för felfunktionen som är mycket nära den som SQL Server använder internt:
Ett exempel, för att beräkna CDF för x =30 med normalfördelningen för vår testfråga:
Notera normaliseringssteget för att konvertera till standardnormalfördelningen. Proceduren returnerar värdet 0,2407196…, vilket matchar motsvarande Excel-resultat med sju decimaler.
Följande kod modifierar vår exempelfråga för att producera en större uppskattning för filtret (jämförelsen är nu med värdet 32, vilket är mycket närmare medelvärdet än tidigare):
Uppskattningen från optimeraren är nu 36,7807 .
För att beräkna uppskattningen manuellt måste vi först ta itu med några sista detaljer:
Följande procedur innehåller alla detaljer i den här artikeln. Det kräver CDF-proceduren som gavs tidigare:
Vi kan nu använda denna procedur för att generera en uppskattning för vår nya testfråga:
Utdata är:
Detta kan jämföras mycket bra med optimerarens kardinalitetsuppskattning på 36,7807.
Förfarandet kan användas för andra räkneintervall förutom jämställdhetstest. Allt som krävs är att ställa in
För att använda detta med vår procedur ställer vi in
Resultatet är 572.5964:
Ett sista exempel med
Optimeringsuppskattningen är
Sedan
Återigen stämmer detta överens med optimeringsuppskattningen.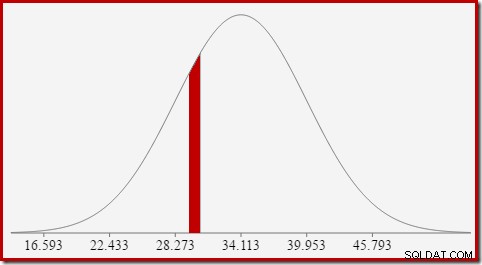
Den kumulativa distributionsfunktionen
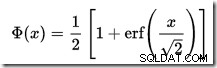
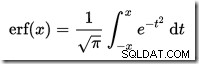
CREATE PROCEDURE dbo.GetStandardNormalCDF
(
@x float,
@cdf float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
DECLARE
@sign float,
@erf float;
SET @sign = SIGN(@x);
SET @x = ABS(@x) / SQRT(2);
SET @erf = 1;
SET @erf = @erf + (0.0705230784 * @x);
SET @erf = @erf + (0.0422820123 * POWER(@x, 2));
SET @erf = @erf + (0.0092705272 * POWER(@x, 3));
SET @erf = @erf + (0.0001520143 * POWER(@x, 4));
SET @erf = @erf + (0.0002765672 * POWER(@x, 5));
SET @erf = @erf + (0.0000430638 * POWER(@x, 6));
SET @erf = POWER(@erf, -16);
SET @erf = 1 - @erf;
SET @erf = @erf * @sign;
SET @cdf = 0.5 * (1 + @erf);
END; DECLARE @cdf float;
DECLARE @x float;
-- HAVING COUNT_BIG(*) = x
SET @x = 30;
-- Normalize 30 by subtracting the mean
-- and dividing by the standard deviation
SET @x = (@x - 34.1113) / 5.84;
EXECUTE dbo.GetStandardNormalCDF
@x = @x,
@cdf = @cdf OUTPUT;
SELECT CDF = @cdf; Sluta detaljer och exempel
SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) = 32;
COUNT(*) = 1 , som inte beskrivs i detalj här. COUNT(*) = 1 fall använder den äldre CE:n samma logik som den nya CE:n (tillgänglig i SQL Server 2014 och framåt).CREATE PROCEDURE dbo.GetCountPredicateEstimate
(
@From integer,
@To integer,
@Cardinality float,
@Density float,
@Selectivity float OUTPUT,
@Estimate float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
BEGIN TRY
DECLARE
@Start float,
@End float,
@Distinct float,
@Mean float,
@MeanAdj float,
@Stdev float,
@NormStart float,
@NormEnd float,
@CDFStart float,
@CDFEnd float;
-- Validate input and apply defaults
IF ISNULL(@From, 0) = 0 SET @From = 1;
IF @From < 1 RAISERROR ('@From must be >= 1', 16, 1);
IF ISNULL(@Cardinality, -1) <= 0 RAISERROR('@Cardinality must be positive', 16, 1);
IF ISNULL(@Density, -1) <= 0 RAISERROR('@Density must be positive', 16, 1);
IF ISNULL(@To, 0) = 0 SET @To = CEILING(1 / @Density);
IF @To < @From RAISERROR('@To must be >= @From', 16, 1);
-- Convert integer range to interval
SET @Start = @From - 0.5;
SET @End = @To + 0.5;
-- Get number of distinct values
SET @Distinct = 1 / @Density;
-- Calculate mean
SET @Mean = @Cardinality * @Density;
-- Adjust mean;
SET @MeanAdj = @Mean * ((@Distinct - 1) / @Distinct);
-- Get standard deviation (guess)
SET @Stdev = SQRT(@MeanAdj);
-- Normalize interval
SET @NormStart = (@Start - @Mean) / @Stdev;
SET @NormEnd = (@End - @Mean) / @Stdev;
-- Calculate CDFs
EXECUTE dbo.GetStandardNormalCDF
@x = @NormStart,
@cdf = @CDFStart OUTPUT;
EXECUTE dbo.GetStandardNormalCDF
@x = @NormEnd,
@cdf = @CDFEnd OUTPUT;
-- Selectivity
SET @Selectivity =
CASE
-- Unbounded start
WHEN @From = 1 THEN @CDFEnd
-- Unbounded end
WHEN @To >= @Distinct THEN 1 - @CDFStart
-- Normal interval
ELSE @CDFEnd - @CDFStart
END;
-- Return row estimate
SET @Estimate = @Selectivity * @Distinct;
END TRY
BEGIN CATCH
DECLARE @EM nvarchar(4000) = ERROR_MESSAGE();
IF @@TRANCOUNT > 0 ROLLBACK TRANSACTION;
RAISERROR (@EM, 16, 1);
RETURN;
END CATCH;
END; DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = 32,
@To = 32,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
Exempel på ojämlikhetsintervall
@From och @To parametrar till heltalsintervallgränserna. För att ange obegränsad, skicka noll eller NULL som du föredrar.SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) < 50;

@From = NULL och @To = 49 (eftersom 50 exkluderas med mindre än):DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = NULL,
@To = 49,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
BETWEEN :SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) BETWEEN 25 AND 30;

BETWEEN är inklusive, klarar vi proceduren @From = 25 och @To = 30 . Resultatet är:
