I den här artikeln fortsätter jag täckningen av lösningar på Peter Larssons lockande matchande utmaning för utbud och efterfrågan. Tack igen till Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie och Peter Larsson, för att du skickade dina lösningar.
Förra månaden täckte jag en lösning baserad på intervallkorsningar, med ett klassiskt predikatbaserat intervallskärningstest. Jag hänvisar till den lösningen som klassiska korsningar . Den klassiska intervallskärningsmetoden resulterar i en plan med kvadratisk skalning (N^2). Jag visade dess dåliga prestanda mot provingångar som sträcker sig från 100K till 400K rader. Det tog lösningen 931 sekunder att slutföra mot ingången på 400 000 rader! Den här månaden börjar jag med att kort påminna dig om förra månadens lösning och varför den skalar och presterar så dåligt. Jag kommer sedan att introducera ett tillvägagångssätt baserat på en revidering av intervallskärningstestet. Detta tillvägagångssätt användes av Luca, Kamil och möjligen även Daniel, och det möjliggör en lösning med mycket bättre prestanda och skalning. Jag hänvisar till den lösningen som reviderade korsningar .
Problemet med det klassiska korsningstestet
Låt oss börja med en snabb påminnelse om förra månadens lösning.
Jag använde följande index på input dbo.Auktionstabellen för att stödja beräkningen av de löpande summorna som producerar efterfråge- och utbudsintervall:
-- Index to support solution CREATE UNIQUE NONCLUSTERED INDEX idx_Code_ID_i_Quantity ON dbo.Auctions(Code, ID) INCLUDE(Quantity); -- Enable batch-mode Window Aggregate CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs ON dbo.Auctions(ID) WHERE ID = -1 AND ID = -2;
Följande kod har den kompletta lösningen som implementerar den klassiska interval intersections-metoden:
-- Drop temp tables if exist
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
WITH D0 AS
-- D0 computes running demand as EndDemand
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
FROM dbo.Auctions
WHERE Code = 'D'
),
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
D AS
(
SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
FROM D0
)
SELECT ID,
CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
WITH S0 AS
-- S0 computes running supply as EndSupply
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
FROM dbo.Auctions
WHERE Code = 'S'
),
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
S AS
(
SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
FROM S0
)
SELECT ID,
CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
CREATE UNIQUE CLUSTERED INDEX idx_cl_ES_ID ON #Supply(EndSupply, ID);
-- Trades are the overlapping segments of the intersecting intervals
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
INNER JOIN #Supply AS S WITH (FORCESEEK)
ON D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply; Den här koden börjar med att beräkna efterfråge- och utbudsintervallen och skriva dem till temporära tabeller som kallas #Demand och #Supply. Koden skapar sedan ett klustrat index på #Supply med EndSupply som ledande nyckel för att stödja korsningstestet så bra som möjligt. Slutligen förenar koden #Supply and #Demand, och identifierar affärer som de överlappande segmenten av de skärande intervallen, med hjälp av följande kopplingspredikat baserat på det klassiska interval intersection-testet:
D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply
Planen för denna lösning visas i figur 1.
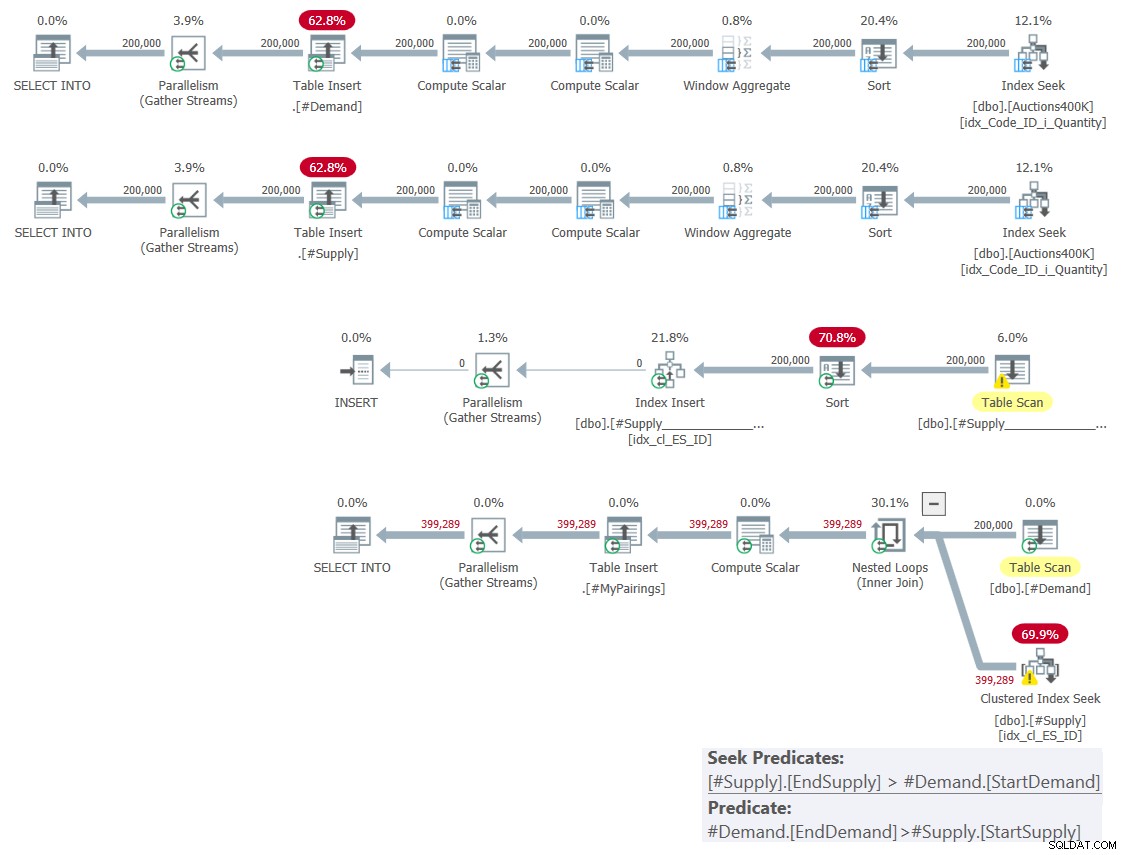Figur 1:Fråga plan för lösning baserad på klassiska korsningar
Som jag förklarade förra månaden, bland de två inblandade intervallpredikaten, kan endast det ena användas som ett sökpredikat som en del av en indexsökningsoperation, medan det andra måste användas som ett restpredikat. Du kan tydligt se detta i planen för den sista frågan i figur 1. Det var därför jag bara brydde mig om att skapa ett index på en av tabellerna. Jag tvingade också att använda en sökning i indexet som jag skapade med hjälp av FORCESEEK-tipset. Annars kan optimeraren sluta ignorera det indexet och skapa ett eget med hjälp av en Index Spool-operator.
Denna plan har kvadratisk komplexitet eftersom per rad på ena sidan—#Demand i vårt fall—indexsökningen kommer att behöva komma åt i genomsnitt hälften av raderna på den andra sidan—#Supply i vårt fall—baserat på sökpredikatet, och identifiera slutliga matcher genom att använda restpredikatet.
Om det fortfarande är oklart för dig varför denna plan har kvadratisk komplexitet, kanske en visuell skildring av arbetet kan hjälpa dig, som visas i figur 2.
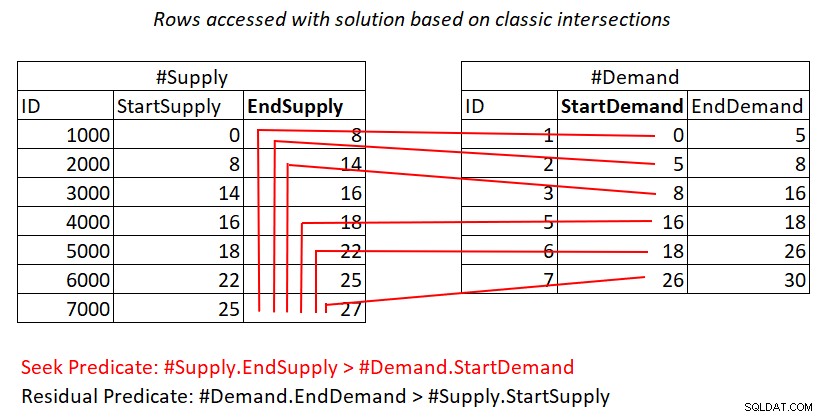Figur 2:Illustration av arbete med lösning baserad på klassiska korsningar
Den här illustrationen representerar det arbete som utförts av de kapslade looparna i planen för den senaste frågan. #Demand-högen är den yttre ingången för kopplingen och det klustrade indexet på #Supply (med EndSupply som ledande nyckel) är den inre ingången. De röda linjerna representerar indexsökningsaktiviteterna som görs per rad i #Demand i indexet på #Supply och raderna de kommer åt som en del av intervallskanningarna i indexbladet. Mot extremt låga StartDemand-värden i #Demand behöver intervallskanningen komma nära alla rader i #Supply. Mot extremt höga StartDemand-värden i #Demand behöver intervallskanningen komma åt nära noll rader i #Supply. I genomsnitt behöver intervallskanningen komma åt ungefär hälften av raderna i #Supply per rad i efterfrågan. Med D efterfrågerader och S utbudsrader är antalet åtkomliga rader D + D*S/2. Det kommer utöver kostnaden för sökningarna som tar dig till de matchande raderna. Till exempel, när du fyller dbo.Auktioner med 200 000 efterfrågerader och 200 000 utbudsrader, översätts detta till att de kapslade slingorna går med åtkomst till 200 000 efterfrågerader + 200 000*200 000/2 utbudsrader, eller 200,000,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0 Det pågår en hel del omsökning av utbudsrader här!
Om du vill hålla fast vid idén med intervallkorsningar men få bra prestanda måste du komma på ett sätt att minska mängden arbete som utförs.
I sin lösning bucketade Joe Obbish intervallerna baserat på den maximala intervalllängden. På så sätt kunde han minska antalet rader som skarvarna behövde för att hantera och förlita sig på batchbearbetning. Han använde det klassiska intervallskärningstestet som ett sista filter. Joes lösning fungerar bra så länge den maximala intervalllängden inte är särskilt hög, men lösningens körtid ökar när den maximala intervalllängden ökar.
Så, vad mer kan du göra...?
Reviderat korsningstest
Luca, Kamil och möjligen Daniel (det var en otydlig del om hans upplagda lösning på grund av webbplatsens formatering, så jag var tvungen att gissa) använde ett reviderat interval intersection-test som möjliggör mycket bättre utnyttjande av indexering.
Deras skärningstest är en disjunktion av två predikat (predikat separerade med OR-operator):
(D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >= D.StartDemand AND S.StartSupply < D.EndDemand)
På engelska skär antingen efterfrågestartavgränsaren utbudsintervallet på ett inkluderande, exklusivt sätt (inklusive början och exklusive slutet); eller så skär utbudsstartavgränsaren efterfrågeintervallet, på ett inkluderande, exklusivt sätt. För att göra de två predikaten disjunkta (inte ha överlappande fall) men ändå kompletta i att täcka alla fall, kan du behålla =-operatorn i bara det ena eller det andra, till exempel:
(D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand)
Detta reviderade intervallskärningstest är ganska insiktsfullt. Vart och ett av predikaten kan potentiellt effektivt använda ett index. Överväg predikat 1:
D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply ^^^^^^^^^^^^^ ^^^^^^^^^^^^^
Förutsatt att du skapar ett täckande index på #Demand med StartDemand som ledande nyckel, kan du potentiellt få en Nested Loops-join genom att tillämpa arbetet som illustreras i figur 3.
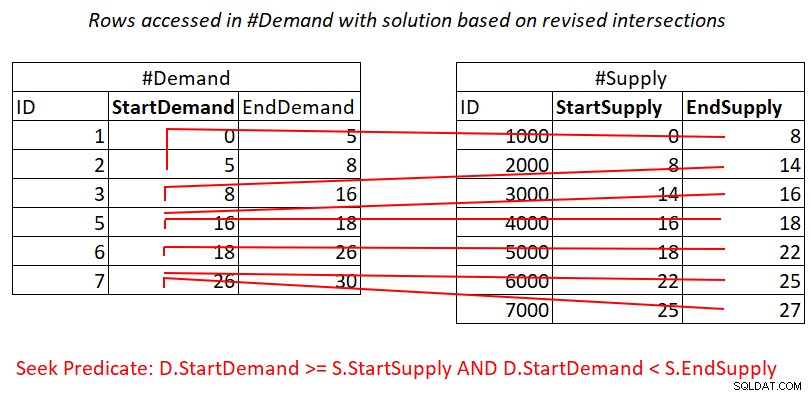
Figur 3:Illustration av teoretiskt arbete som krävs för att bearbeta predikat 1
Ja, du betalar fortfarande för en sökning i #Demand-indexet per rad i #Supply, men intervallet skannar i indexbladet kommer åt nästan osammanhängande delmängder av rader. Ingen omsökning av rader!
Situationen är liknande med predikat 2:
S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand ^^^^^^^^^^^^^ ^^^^^^^^^^^^^
Förutsatt att du skapar ett täckande index på #Supply med StartSupply som ledande nyckel, kan du potentiellt få en Nested Loops-join genom att tillämpa det arbete som illustreras i figur 4.
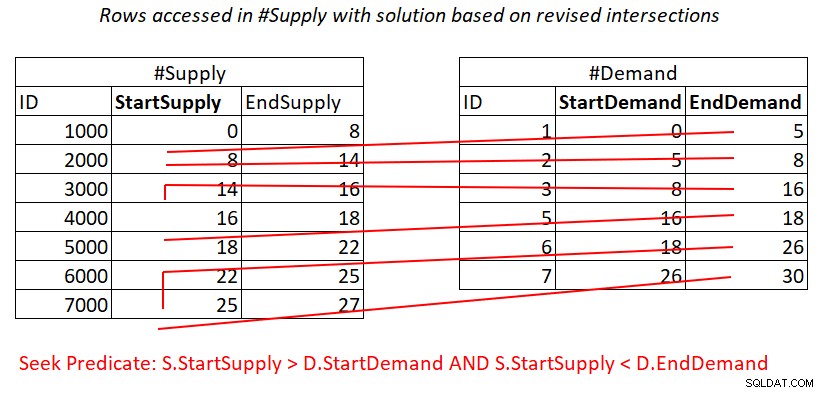
Figur 4:Illustration av teoretiskt arbete som krävs för att bearbeta predikat 2
Här betalar du också för en sökning i #Supply index per rad i #Demand, och sedan skannar intervallet i indexbladet åtkomst till nästan osammanhängande delmängder av rader. Återigen, ingen omsökning av rader!
Om man antar D efterfrågerader och S utbudsrader kan arbetet beskrivas som:
Number of index seek operations: D + S Number of rows accessed: 2D + 2S
Så troligtvis är den största delen av kostnaden här I/O-kostnaden involverad i sökningarna. Men den här delen av arbetet har linjär skalning jämfört med den kvadratiska skalningen i den klassiska intervallskärningsfrågan.
Naturligtvis måste du ta hänsyn till den preliminära kostnaden för indexskapandet på de tillfälliga tabellerna, som har n log n-skalning på grund av sorteringen det handlar om, men du betalar denna del som en preliminär del av båda lösningarna.
Låt oss försöka omsätta denna teori i praktiken. Låt oss börja med att fylla i de temporära tabellerna #Demand och #supply med efterfråge- och utbudsintervallen (samma som med de klassiska intervallkorsningarna) och skapa de stödjande indexen:
-- Drop temp tables if exist
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
WITH D0 AS
-- D0 computes running demand as EndDemand
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
FROM dbo.Auctions
WHERE Code = 'D'
),
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
D AS
(
SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
FROM D0
)
SELECT ID,
CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
WITH S0 AS
-- S0 computes running supply as EndSupply
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
FROM dbo.Auctions
WHERE Code = 'S'
),
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
S AS
(
SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
FROM S0
)
SELECT ID,
CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
-- Indexing
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID); Planerna för att fylla i de tillfälliga tabellerna och skapa indexen visas i figur 5.
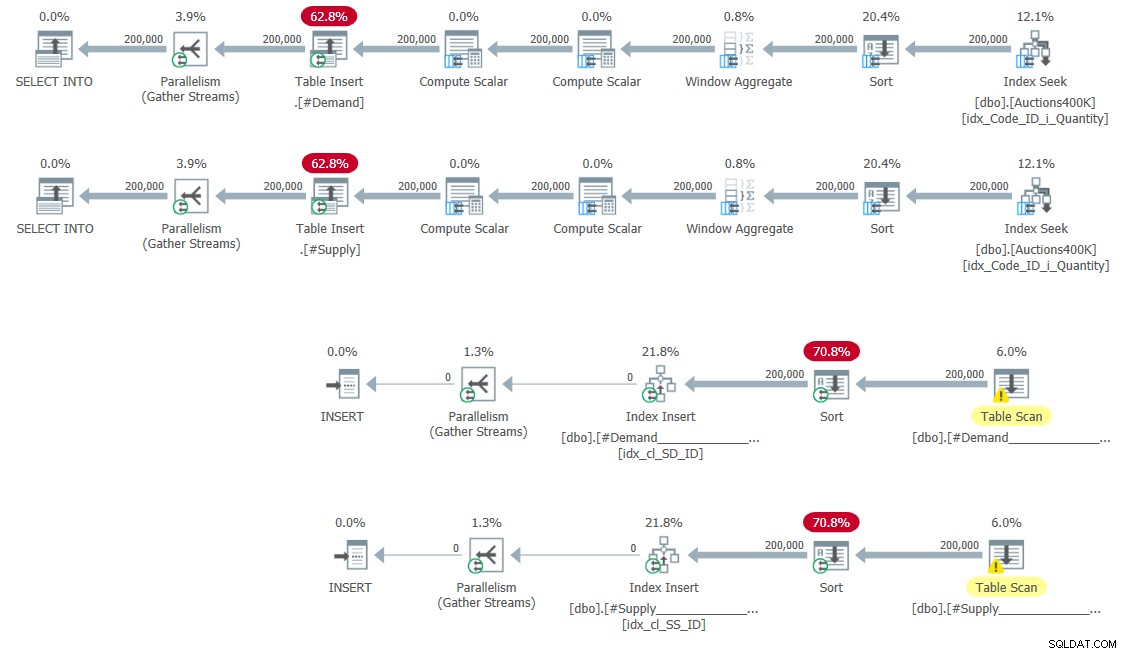
Figur 5:Fråga planer för att fylla i temporära tabeller och skapa index
Inga överraskningar här.
Nu till den sista frågan. Du kan bli frestad att använda en enda fråga med ovannämnda disjunktion av två predikat, som så:
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
INNER JOIN #Supply AS S
ON (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand); Planen för denna fråga visas i figur 6.
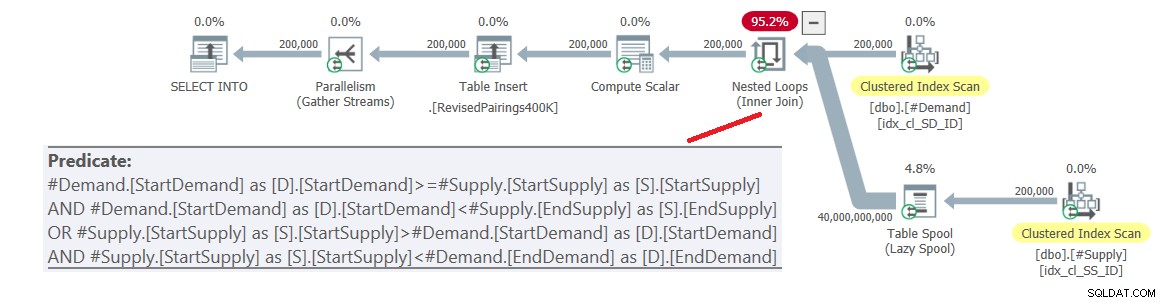
Figur 6:Frågeplan för slutlig fråga med reviderad skärningspunkt testa, prova 1
Problemet är att optimeraren inte vet hur man delar upp denna logik i två separata aktiviteter, som var och en hanterar ett annat predikat och använder respektive index effektivt. Så det slutar med en fullständig kartesisk produkt av de två sidorna, och tillämpar alla predikat som restpredikat. Med 200 000 efterfrågerader och 200 000 utbudsrader bearbetar kopplingen 40 000 000 000 rader.
Det insiktsfulla knep som användes av Luca, Kamil och möjligen Daniel var att dela upp logiken i två frågor och förena deras resultat. Det är där det blir viktigt att använda två osammanhängande predikat! Du kan använda en UNION ALL-operatör istället för UNION, vilket undviker den onödiga kostnaden för att leta efter dubbletter. Här är frågan som implementerar detta tillvägagångssätt:
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
INNER JOIN #Supply AS S
ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
UNION ALL
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
FROM #Demand AS D
INNER JOIN #Supply AS S
ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand; Planen för denna fråga visas i figur 7.
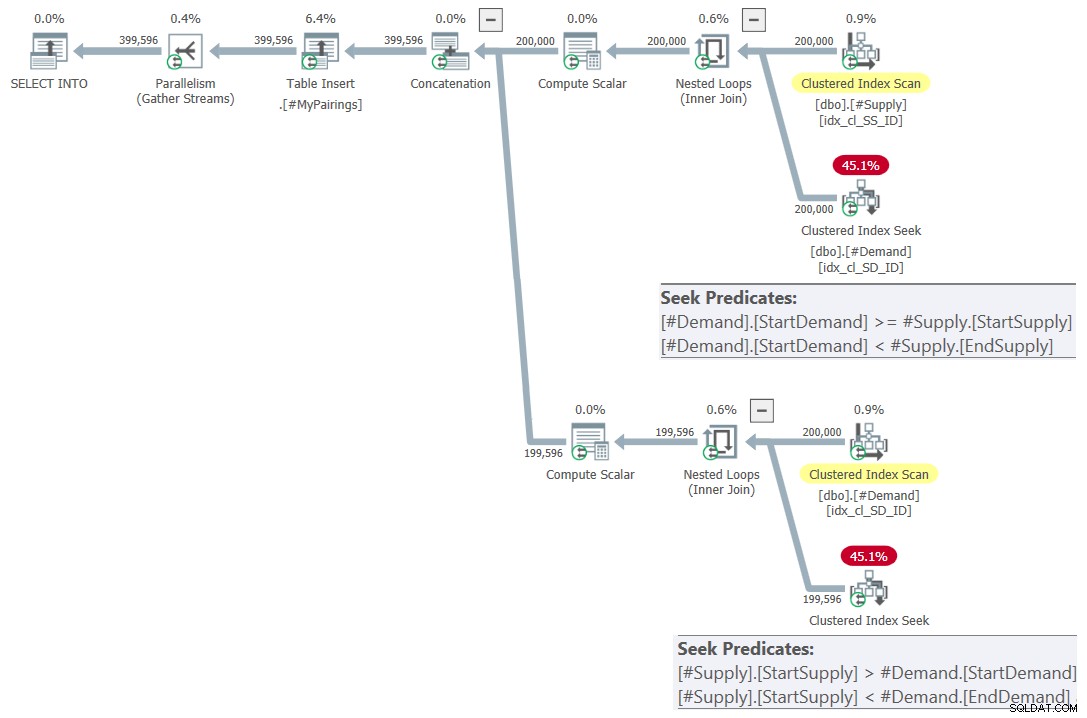
Figur 7:Frågaplan för slutlig fråga med reviderad skärningspunkt testa, prova 2
Det här är bara vackert! är det inte? Och eftersom det är så vackert, här är hela lösningen från början, inklusive skapandet av tillfälliga tabeller, indexering och den slutliga frågan:
-- Drop temp tables if exist
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
WITH D0 AS
-- D0 computes running demand as EndDemand
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
FROM dbo.Auctions
WHERE Code = 'D'
),
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
D AS
(
SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
FROM D0
)
SELECT ID,
CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
WITH S0 AS
-- S0 computes running supply as EndSupply
(
SELECT ID, Quantity,
SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
FROM dbo.Auctions
WHERE Code = 'S'
),
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
S AS
(
SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
FROM S0
)
SELECT ID,
CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
-- Indexing
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);
-- Trades are the overlapping segments of the intersecting intervals
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
INNER JOIN #Supply AS S
ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
UNION ALL
SELECT
D.ID AS DemandID, S.ID AS SupplyID,
CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
AS TradeQuantity
FROM #Demand AS D
INNER JOIN #Supply AS S
ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand; Som nämnts tidigare kommer jag att hänvisa till den här lösningen som reviderade korsningar .
Kamils lösning
Mellan Lucas, Kamils och Daniels lösningar var Kamils snabbaste. Här är Kamils kompletta lösning:
SET NOCOUNT ON;
DROP TABLE IF EXISTS #supply, #demand;
GO
CREATE TABLE #demand
(
DemandID INT NOT NULL,
DemandQuantity DECIMAL(19, 6) NOT NULL,
QuantityFromDemand DECIMAL(19, 6) NOT NULL,
QuantityToDemand DECIMAL(19, 6) NOT NULL
);
CREATE TABLE #supply
(
SupplyID INT NOT NULL,
QuantityFromSupply DECIMAL(19, 6) NOT NULL,
QuantityToSupply DECIMAL(19,6) NOT NULL
);
WITH demand AS
(
SELECT
a.ID AS DemandID,
a.Quantity AS DemandQuantity,
SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW)
- a.Quantity AS QuantityFromDemand,
SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW)
AS QuantityToDemand
FROM dbo.Auctions AS a WHERE Code = 'D'
)
INSERT INTO #demand
(
DemandID,
DemandQuantity,
QuantityFromDemand,
QuantityToDemand
)
SELECT
d.DemandID,
d.DemandQuantity,
d.QuantityFromDemand,
d.QuantityToDemand
FROM demand AS d;
WITH supply AS
(
SELECT
a.ID AS SupplyID,
SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW)
- a.Quantity AS QuantityFromSupply,
SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW)
AS QuantityToSupply
FROM dbo.Auctions AS a WHERE Code = 'S'
)
INSERT INTO #supply
(
SupplyID,
QuantityFromSupply,
QuantityToSupply
)
SELECT
s.SupplyID,
s.QuantityFromSupply,
s.QuantityToSupply
FROM supply AS s;
CREATE UNIQUE INDEX ix_1 ON #demand(QuantityFromDemand)
INCLUDE(DemandID, DemandQuantity, QuantityToDemand);
CREATE UNIQUE INDEX ix_1 ON #supply(QuantityFromSupply)
INCLUDE(SupplyID, QuantityToSupply);
CREATE NONCLUSTERED COLUMNSTORE INDEX nci ON #demand(DemandID)
WHERE DemandID is null;
DROP TABLE IF EXISTS #myPairings;
CREATE TABLE #myPairings
(
DemandID INT NOT NULL,
SupplyID INT NOT NULL,
TradeQuantity DECIMAL(19, 6) NOT NULL
);
INSERT INTO #myPairings(DemandID, SupplyID, TradeQuantity)
SELECT
d.DemandID,
s.SupplyID,
d.DemandQuantity
- CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply
THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 end
- CASE WHEN s.QuantityToSupply < d.QuantityToDemand
THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity
FROM #demand AS d
INNER JOIN #supply AS s
ON (d.QuantityFromDemand < s.QuantityToSupply
AND s.QuantityFromSupply <= d.QuantityFromDemand)
UNION ALL
SELECT
d.DemandID,
s.SupplyID,
d.DemandQuantity
- CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply
THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 END
- CASE WHEN s.QuantityToSupply < d.QuantityToDemand
THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity
FROM #supply AS s
INNER JOIN #demand AS d
ON (s.QuantityFromSupply < d.QuantityToDemand
AND d.QuantityFromDemand < s.QuantityFromSupply); Som du kan se är det mycket nära den reviderade korsningslösningen som jag täckte.
Planen för den slutliga frågan i Kamils lösning visas i figur 8.
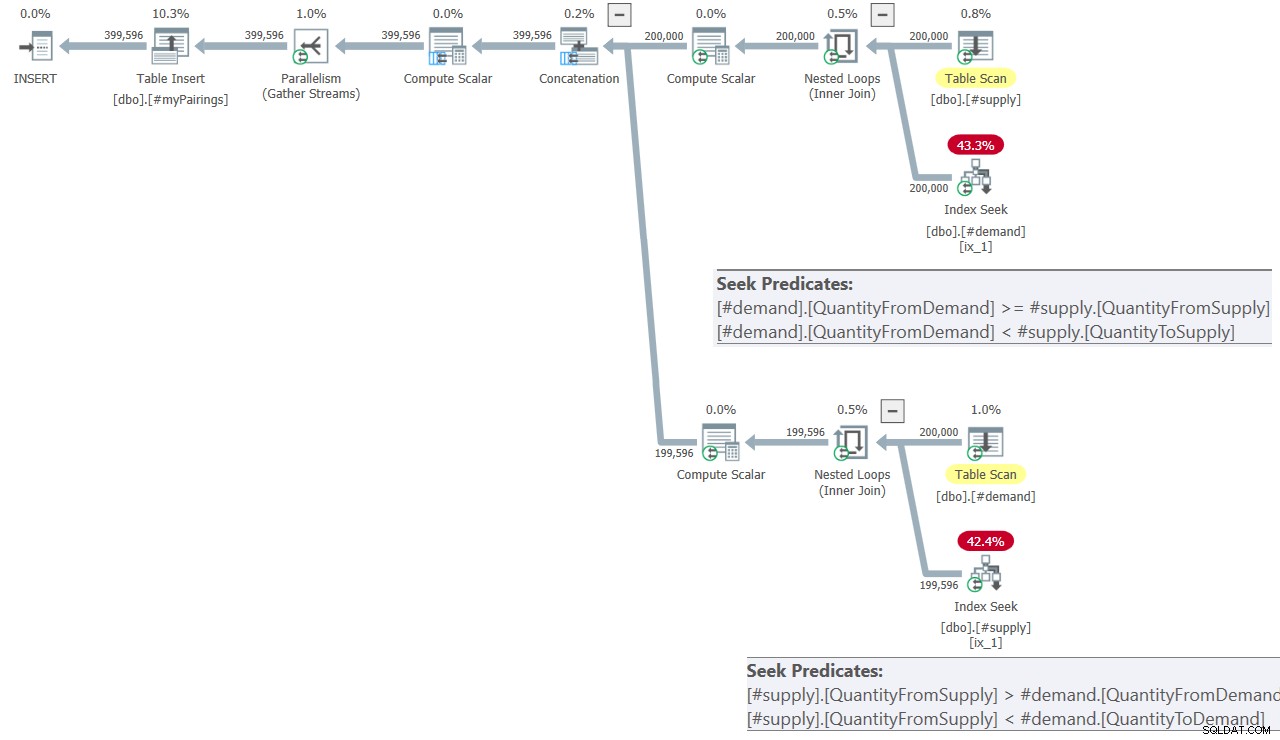
Figur 8:Frågaplan för slutlig fråga i Kamils lösning
Planen ser ganska lik ut den som visades tidigare i figur 7.
Prestandatest
Kom ihåg att den klassiska korsningslösningen tog 931 sekunder att slutföra mot en ingång med 400K rader. Det är 15 minuter! Det är mycket, mycket värre än markörlösningen, som tog cirka 12 sekunder att slutföra mot samma ingång. Figur 9 har prestandasiffrorna inklusive de nya lösningarna som diskuteras i den här artikeln.
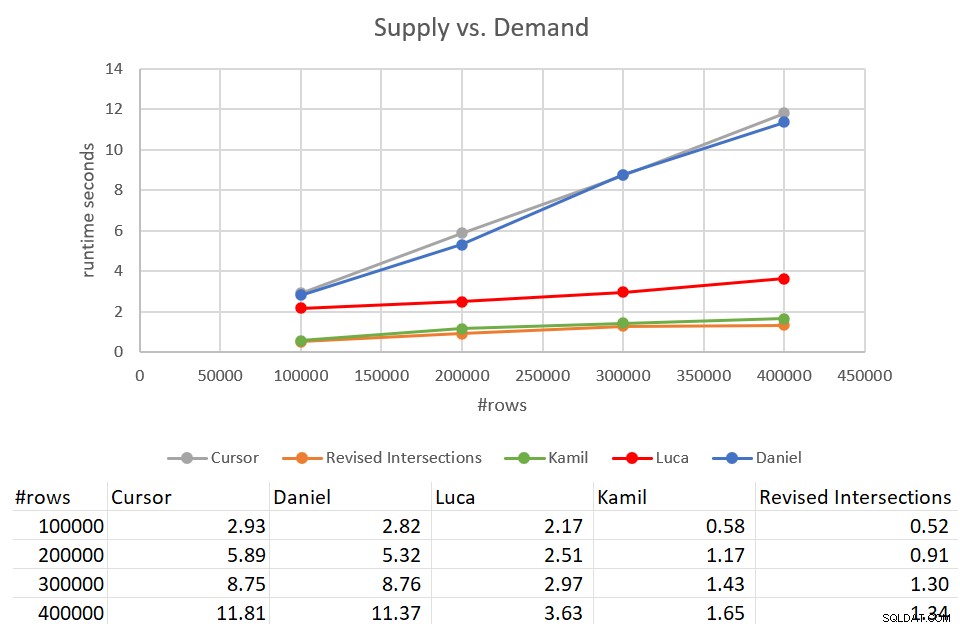
Figur 9:Prestandatest
Som du kan se tog Kamils lösning och den liknande reviderade korsningslösningen cirka 1,5 sekunder att slutföra mot ingången på 400 000 rader. Det är en ganska anständig förbättring jämfört med den ursprungliga markörbaserade lösningen. Den största nackdelen med dessa lösningar är I/O-kostnaden. Med en sökning per rad, för en ingång på 400 000 rader, utför dessa lösningar ett överskott på 1,35 miljoner avläsningar. Men det kan också anses vara en helt acceptabel kostnad med tanke på den goda körtid och skalning du får.
Vad är härnäst?
Vårt första försök att lösa utmaningen med att matcha utbud och efterfrågan förlitade sig på det klassiska interval intersection-testet och fick en dåligt presterande plan med kvadratisk skalning. Mycket värre än den markörbaserade lösningen. Baserat på insikter från Luca, Kamil och Daniel, med ett reviderat intervallskärningstest, var vårt andra försök en betydande förbättring som använder indexering effektivt och presterar bättre än den markörbaserade lösningen. Denna lösning innebär dock en betydande I/O-kostnad. Nästa månad fortsätter jag att utforska ytterligare lösningar.
[ Hoppa till:Ursprunglig utmaning | Lösningar:Del 1 | Del 2 | Del 3 ]